목차
이번 포스트에서는 네트워크 데이터 분석의 기초가 되는 개념들을 다뤄보겠습니다.
1. 그래프의 구성 요소
네트워크 데이터란 두 관측치 사이의 연결성을 나타내는 데이터로, 그래프의 형태로 표현됩니다.
그래프는 N개의 노드 (node) 와 노드들을 잇는 edge들로 정의할 수 있습니다. 앞으로 ($i$,$j$)는 노드 $i$와 노드 $j$를 잇는 edge로 정의하겠습니다. 이 경우, 두 노드 $i$, $j$ 는 인접 (adjacent) 하다고 합니다.
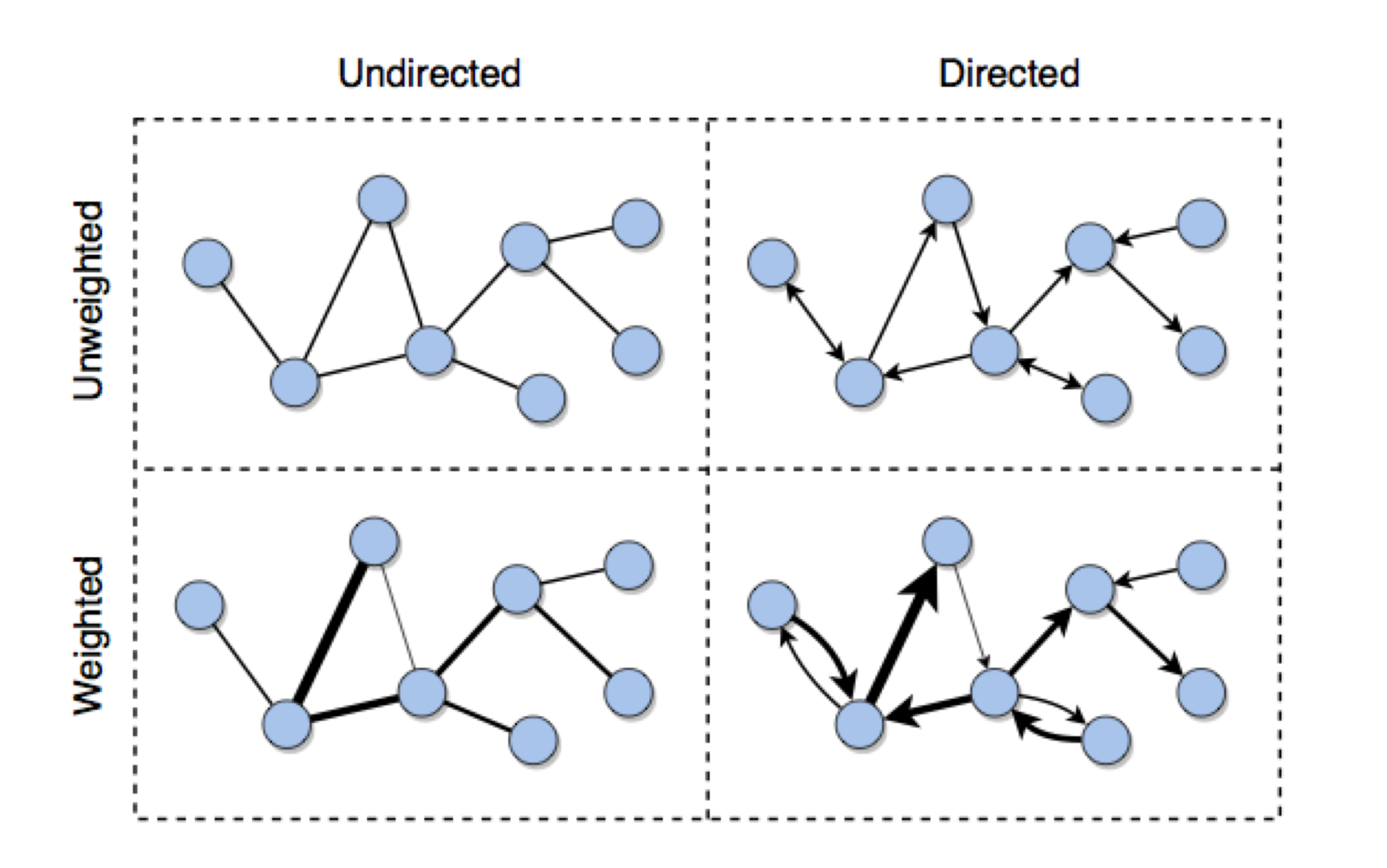
네트워크의 edge는 방향성이 있는 경우 (directed)와 방향성이 없는 경우 (undirected)로 나뉩니다. Undirected graph의 edge ($i$,$j$)는 $i$를 시작점으로 해서 $j$로 간다는 의미입니다.
또한, 네트워크는 unweighted network와 weighted network로 나뉠 수 있습니다. Weighted network의 edge ($i$, $j$, $w$)는 $i$와 $j$를 잇고, w만큼의 weight을 갖는다는 의미입니다.
2. 특별한 네트워크들
네트워크는 형태와 특징에 따라 여러 종류로 나뉘지만, 여기서는 간단하게 두 가지의 특별한 네트워크를 생각해보겠습니다.
2 - 1. Bipartite network
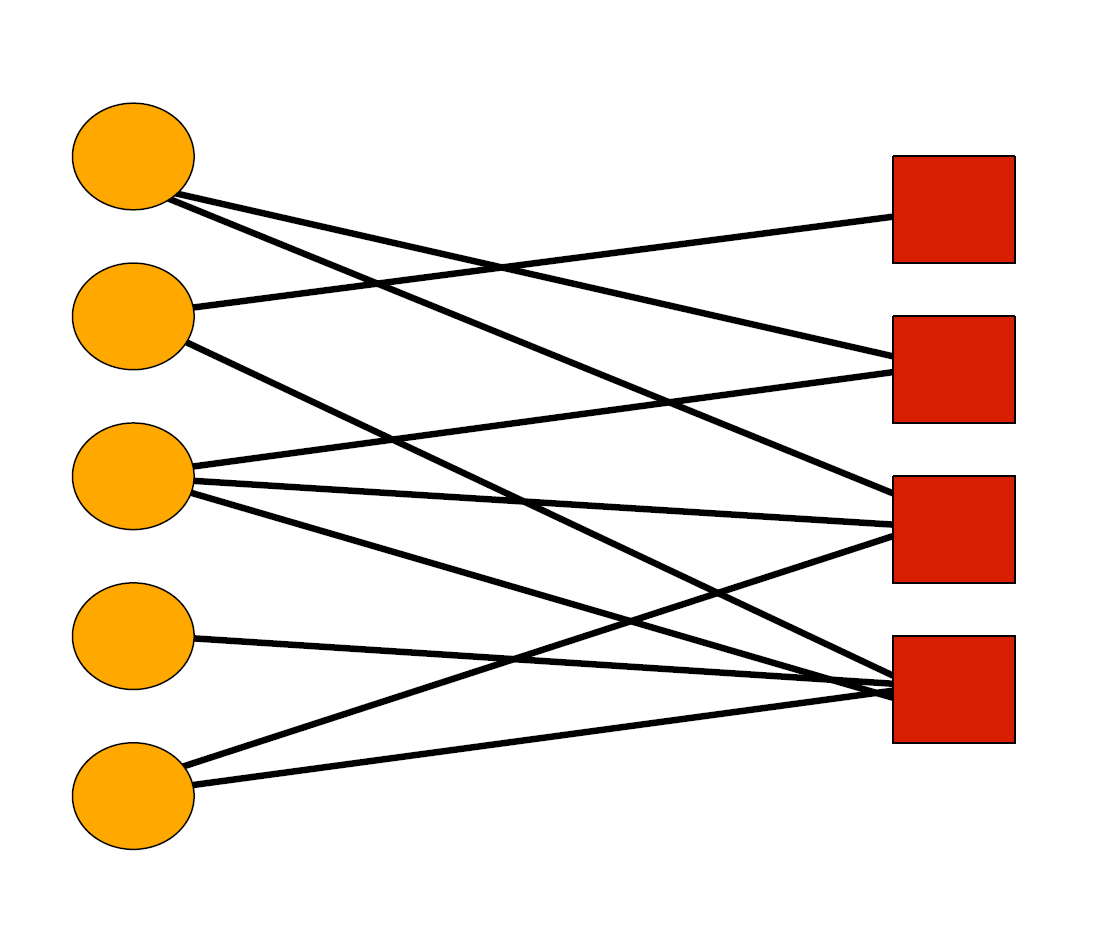
Bipartite network에는 서로 다른 두 그룹의 node들이 존해하고, edge는 서로 다른 그룹에 속한 두 node 사이에서만 정의됩니다. 이러한 네트워크의 예시로는 학생들과 학생들이 수강하는 강의들이 있습니다.
2 - 2. Complete network
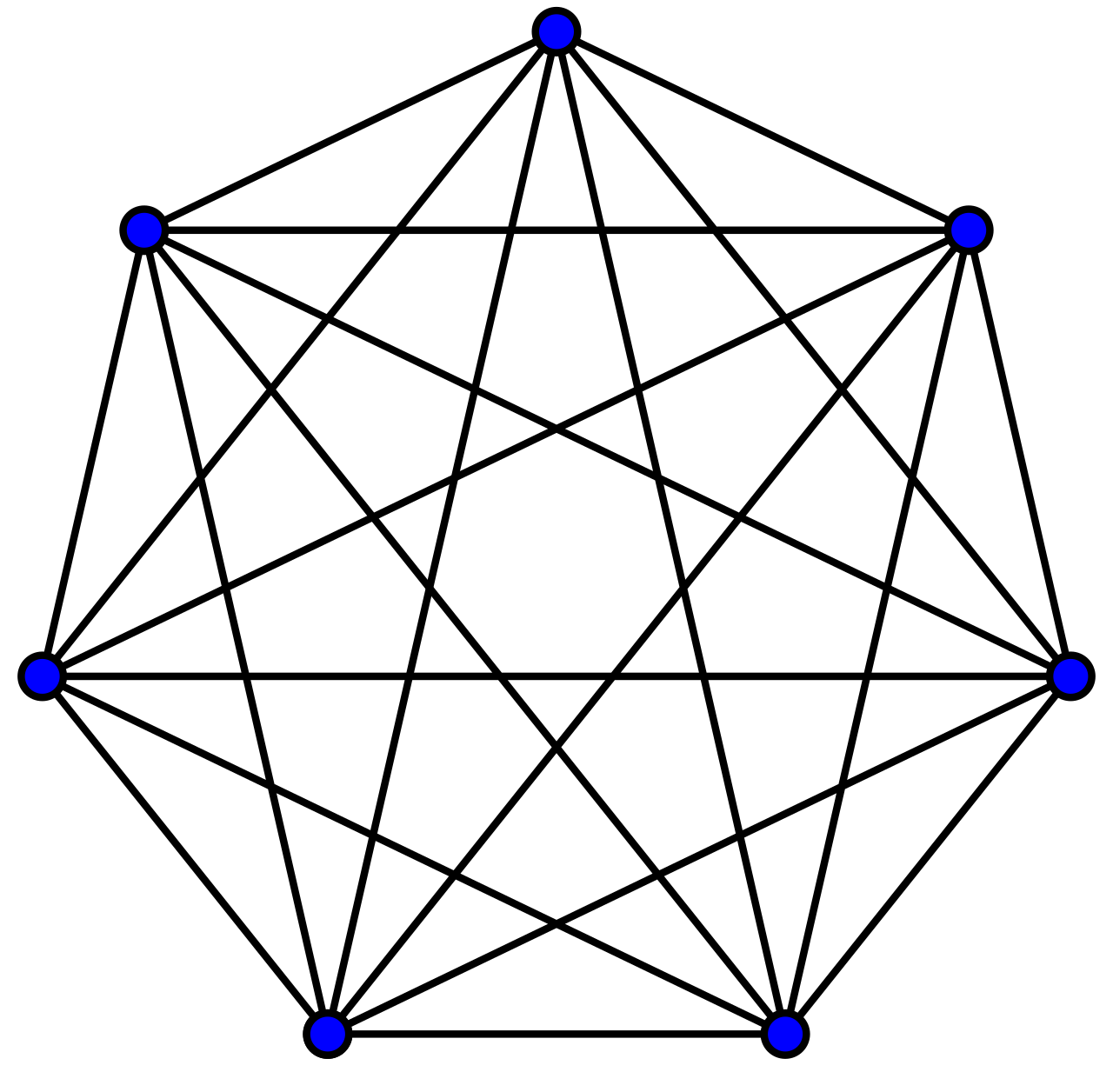
Complete network는 각 node가 다른 모든 node에 연결되어있는 그래프입니다. 즉, node가 주어졌을 때, 달성 가능한 최대의 edge의 개수를 가지고 있는 network입니다. Complete network를 기준으로 네트워크의 다양한 measurement가 정의될 수 있기 때문에 중요합니다.
3. 네트워크의 기본 개념들
앞으로 $N$ = 네트워크의 노드의 개수, $L$ = edge의 수 라고 하겠습니다.
그러면 undirected graph에서 만들어질 수 있는 최대의 edge의 개수는 $L_{max}=\binom{N}{2}=\frac{N(N-2)}{2}$ 입니다.
3 - 1. Density
네트워크의 밀도 (density)는 다음과 같이 정의합니다.
$$d=\frac{L}{L_{max}}=\frac{2L}{N(N-1)}$$
즉, 네트워크의 edge의 개수와 최대로 달성 가능한 edge의 개수의 비율입니다.
보통 $d << 1$이면 네트워크가 sparse 하다고 합니다.
Directed graph의 경우는 최대로 얻을 수 있는 edge의 개수가 $L_{max} = N(N-1)$ 입니다.
따라서, directed graph의 density는 다음과 같습니다.
$$d=\frac{L}{L_{max}}=\frac{L}{N(N-1)}$$
3 - 2. Subnetwork
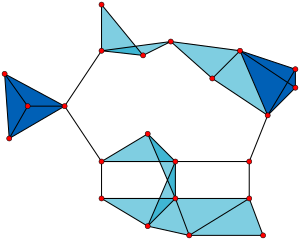
Subnetwork는 주어진 network의 노드의 부분집합과 이 부분집합 사이의 edge들로 정의됩니다. 말 그대로 주워진 네트워크의 일부분입니다.
Clique는 complete한 subnetwork입니다.
3 - 3. Degree
노드 $i$의 degree $k_{i}$는 그 노드에 연결된 edge의 개수, 또는 인접한 node의 개수입니다. Edge가 하나도 연결되지 않은 node는 singleton 이라고 부릅니다.
Directed network에서 degree는 두 가지로 정의됩니다.
노드 $i$의 in-degree $k^{in}_{i}$는 노드 $i$로 들어오는 edge의 개수이고, 노드 $i$의 out-degree $k^{out}_{i}$는 노드 $i$에서부터 나가는 edge의 개수 입니다.
3 - 4. Strength
Weighted network에서는 strength를 다음과 같이 정의할 수 있습니다.
$$s_{i}=\sum_{j}w_{ij}$$
즉, degree의 weighted sum이라고 볼 수 있습니다.
Weighted directed network에서는 strength가 두 가지로 정의됩니다.
in-strength: $s_{i}^{in}=\sum_{j}w_{ji}$
out-strength: $s_{i}^{out}=\sum_{j}w_{ij}$
3 - 5. Average degree
네트워크의 평균 degree는 다음과 같이 정의됩니다.
$$<k> = \frac{\sum_{i}k_{i}}{N}$$
위에서 살펴본 개념들을 종합하면 average degree에 대해 다음과 같은 관계식을 얻을 수 있습니다.
$$<k> = \frac{2L}{N}=\frac{dN(N-1)}{N}=d(N-1)$$
따라서, degree는 다음과 같이 자연스럽게 average degree로 표현됩니다.
$$d=\frac{<k>}{N-1}$$
3 - 6. Multilayer network
네트워크는 여러개의 layer를 가질 수 있습니다. Layer는 네트워크가 정의 되는 또 다른 공간이라고 보시면 됩니다.
예를 들어, 하나의 layer엔 유저들의 페이스북 친구 관계 network을 나타내고, 다른 layer에는 유저들의 인스타그램 팔로우 network를 정의할 수 있습니다.
이 경우, interlayer link 또는 interlayer edge는 같은 layer 안에서 정의되는 edge이고, interlayer link 또는 interlayer edge는 서로 다른 layer 사이에 걸쳐서 연결된 edge를 의미합니다.
각각의 layer에 있는 node들이 동일한 경우, 이 네트워크를 multiplex라고 부릅니다.
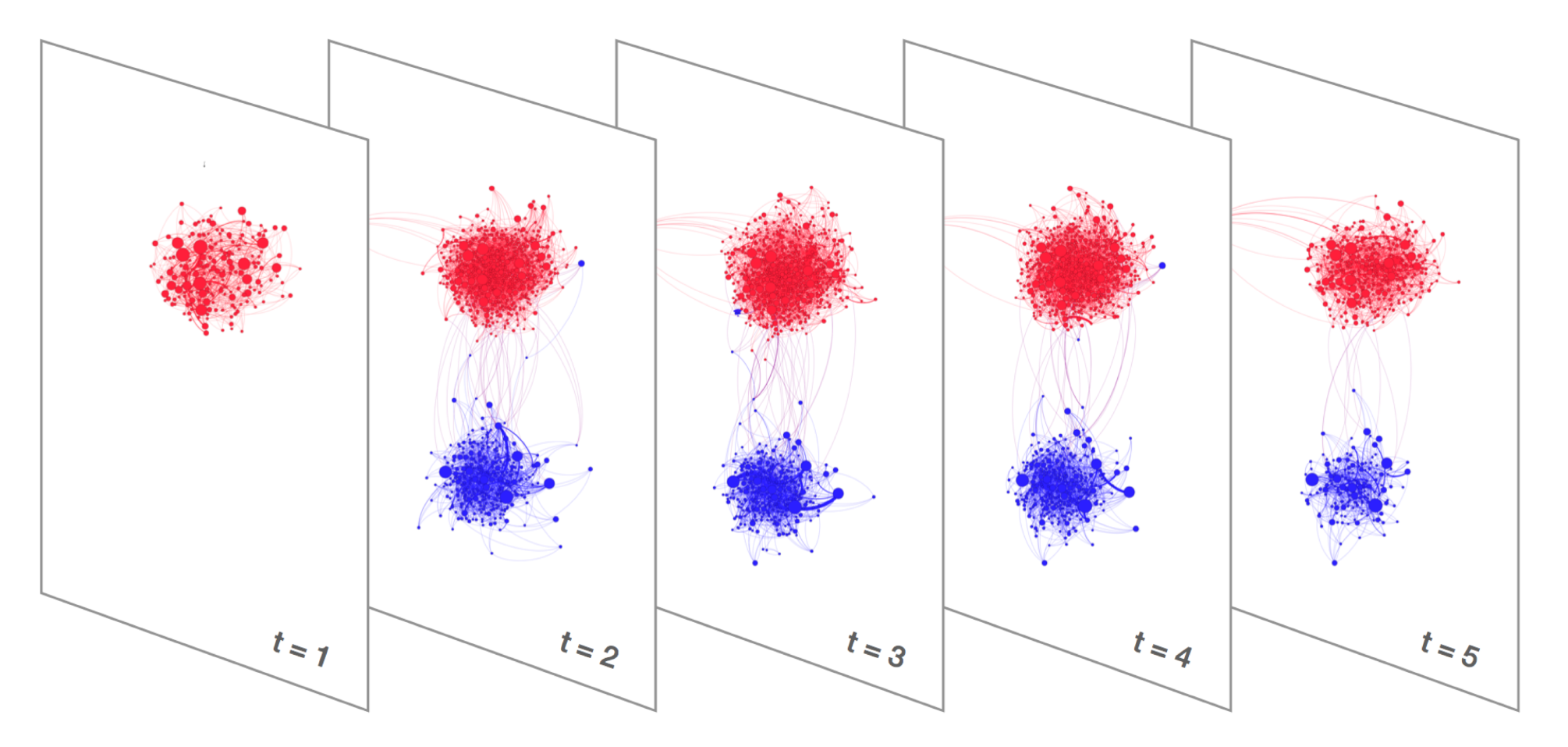
Multiplex의 예로는 temporal network가 있습니다. 이 경우, 각 layer는 시간에 흐름에 따라 찍힌 네트워크의 snapshot이라고 이해하시면 됩니다.
4. 앞으로의 가정들 (assumptions)
1. single-layer 네트워크만 다루도록 하겠습니다.
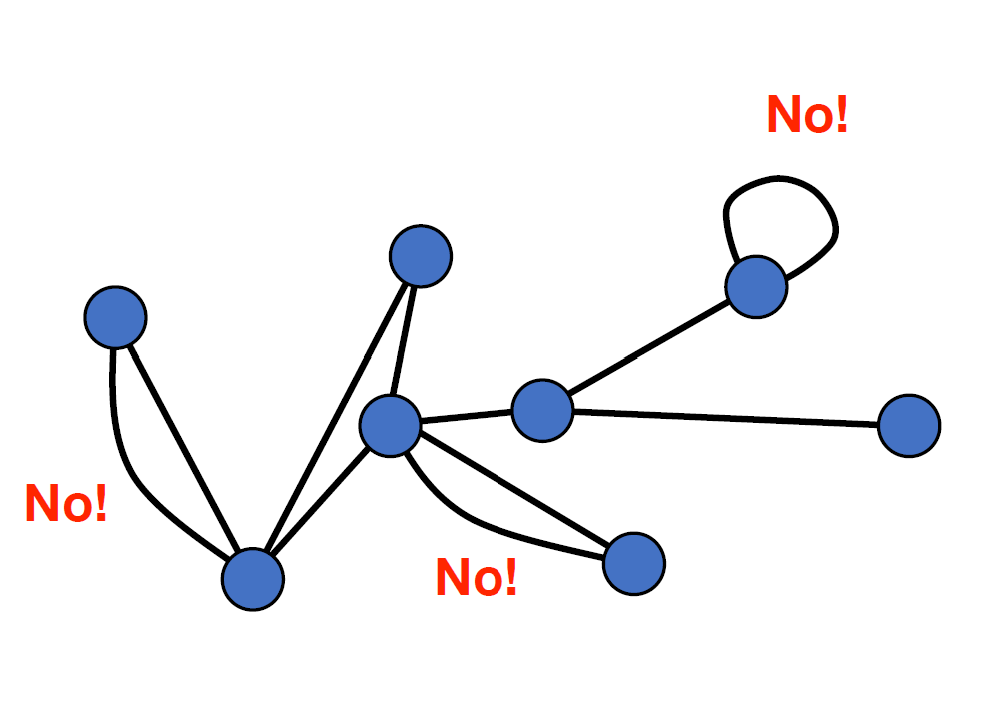
2. 네트워크에 self-loop는 없습니다. 즉, 한 노드에서 같은 노드로 가는 edge는 존재하지 않습니다.
3. 노드와 노드 사이에는 최대 1개의 edge만 존재합니다. 물론, directed graph에서는 $i$와 $j$ 사이에 $(i ,j)$ 와 $(j,i)$ 두개의 edge가 존재할 수 있습니다.
5. 네트워크의 표현 (representations)
5 - 1. Adjacency matrix
Adjacency matrix는 $N \times N$ 행렬로 각 요소 $a_{ij}=1$은 node $i$와 node $j$가 연결되었음을 의미합니다. $a_{ij}=0$은 i와 j가 연결되지 않았음을 나타냅니다. 위의 4의 가정을 만족한다면, adjacency matrix는 다음의 특징을 가집니다.
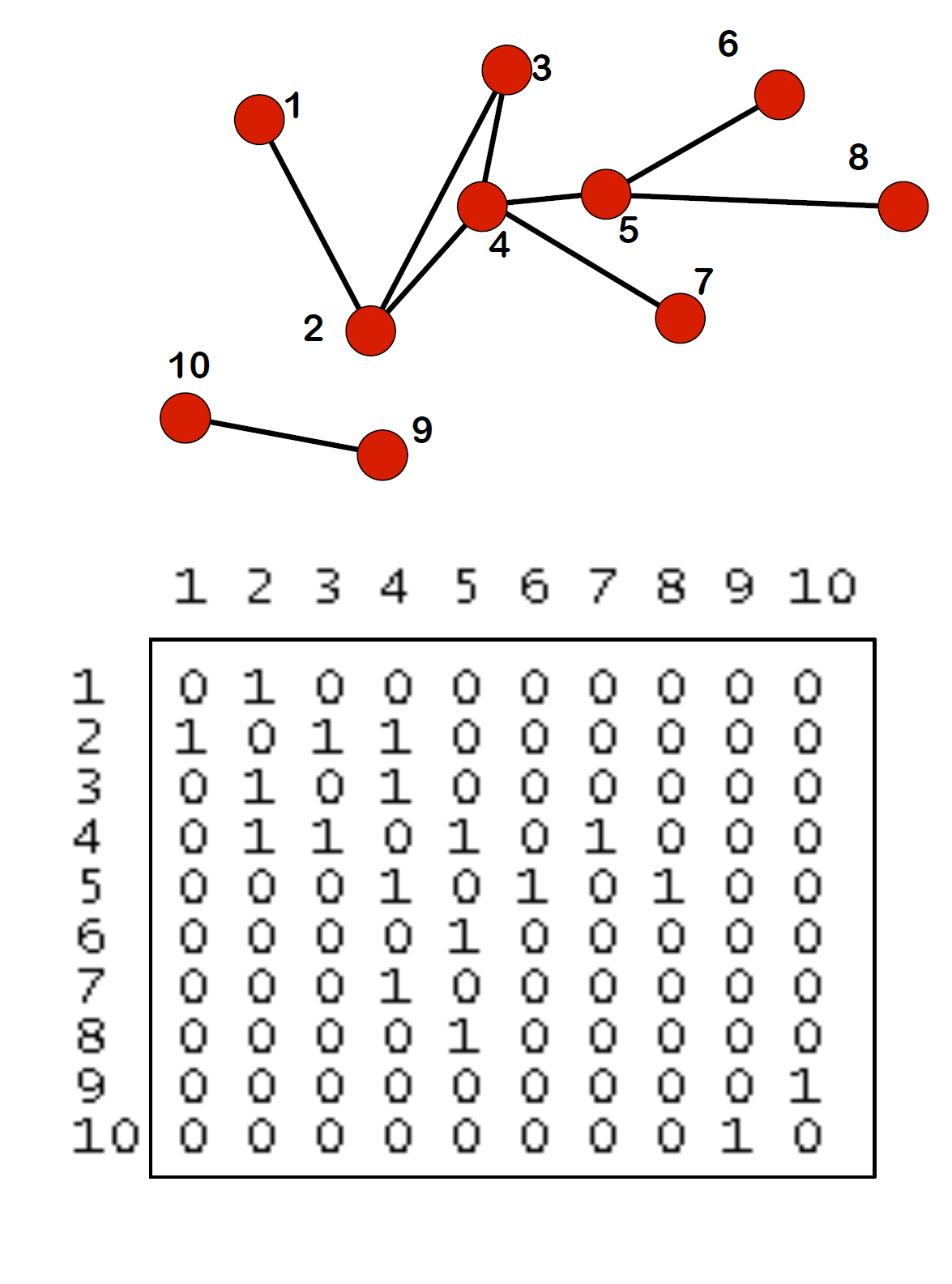
(1) 행렬의 대각선은 모두 0 이다. (self-loop이 없기 때문)
(2) Undirected network에서 adjacency matrix는 대칭이다. ($a_{ij} = a_{ji}$)
(3) Undirected network면, 주어진 node $i$의 degree는 adjacency matrix의 $i$번째 행 또는 열의 요소들의 합이다.
$$k_{i} = \sum_{j}a_{ij} = \sum_{j}a_{ji}$$
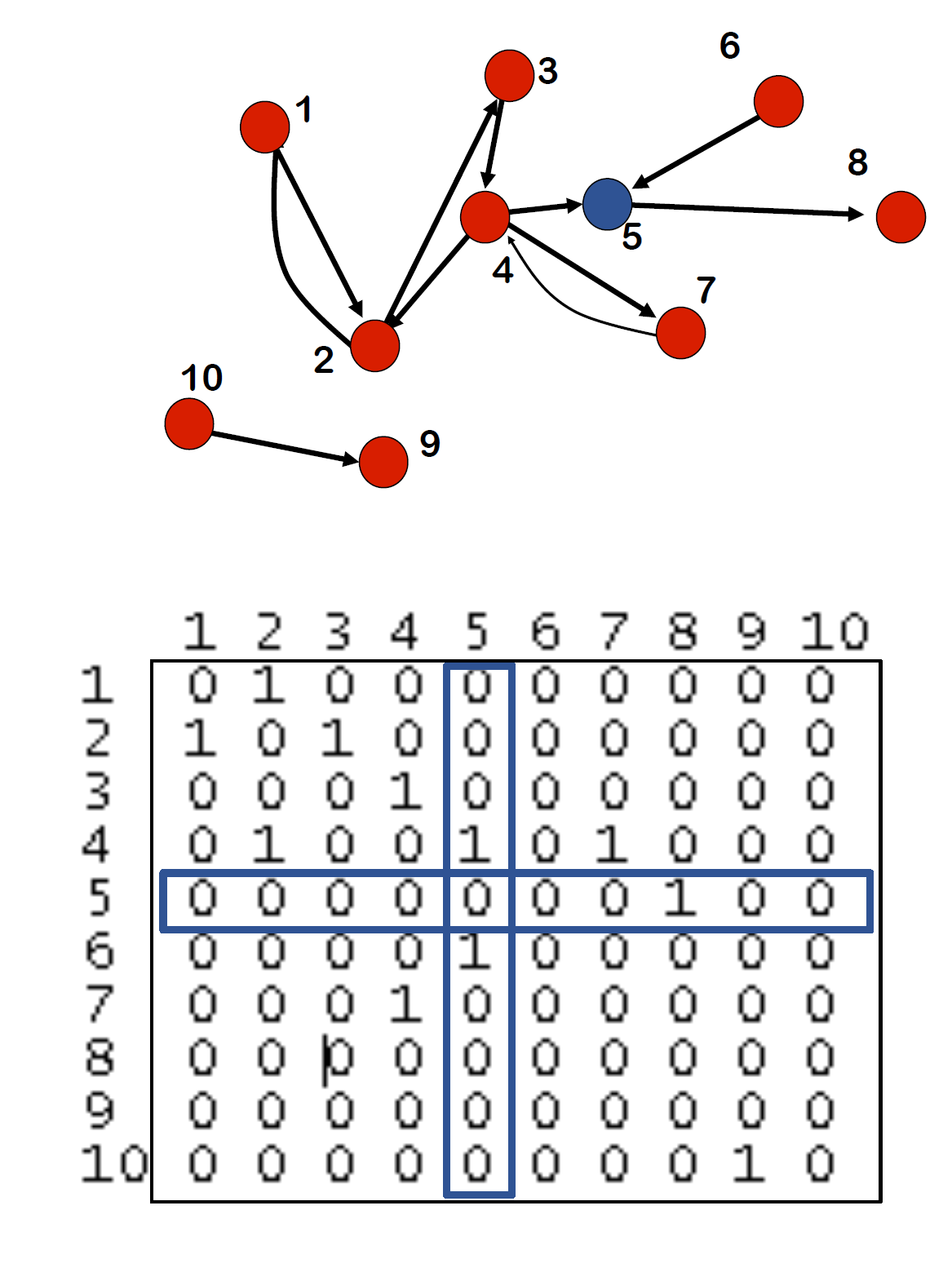
(4) Directed network이면, adjacency matrix는 대칭이 아닐 수도 있다.
(5) $i$의 out-degree는 행렬의 $i$번째 행의 요소들의 합이다.
$$k_{i}^{out}= \sum_{j}a_{ij}$$
(6) $i$의 in-degree는 행렬의 $i$번째 열의 요소들의 합이다.
$$k_{i}^{in}= \sum_{j}a_{ji}$$
5 - 2. Adjacency list
Adjacency matrix의 경우, $N^{2}$의 데이터가 저장되어야 한다. 만약, 네트워크의 edge의 개수가 적다면 (sparse) adjacency matrix는 데이터 저장에 있어서 매우 비효율적일 수도 있습니다. 특히, 대규모 네트워크의 경우, adjacency matrix의 형태로 데이터를 저장한다는 것은 거의 불가능에 가깝죠. 따라서, 보통 edge에 대한 정보만 저장하면 데이터 저장에 있어서 효율적입니다. 왜냐하면 존재하지 않는 edge들은 저장을 할 필요가 없기 때문입니다.
Adjacency list는 각 노드의 이웃 (neighbor)을 리스트를 저장하는 형태입니다. 따라서, undirected network라면, 각 edge는 2번 기록됩니다. 만약 weighted network라면 각 노드의 이웃은 ( neighbor, weight)의 쌍으로 대체됩니다.
5 - 3. Edge list
Edge list는 말 그대로 연결된 노드들의 pair를 저장하는 방식입니다. Weighted network라면 각 pair는 $(i, j, weight)$의 triple로 대체됩니다.


'데이터 사이언스' 카테고리의 다른 글
| 네트워크 데이터 분석 - 현실 네트워크의 특징들 (0) | 2024.06.26 |
|---|---|
| 네트워크 데이터 분석 - Networkx (0) | 2024.06.24 |
| Bootstrap으로 신뢰구간 구하기 (1) | 2024.06.18 |
| 잔차(residual)를 이용한 Bootstrapping (0) | 2021.12.25 |
 Skypainter
Skypainter