목차
이번 포스트에서는 현실 네트워크의 가장 큰 특징인 assortativity (동류성), small world, friend of friend를 다뤄보고자 합니다.
1. Assortativity (동류성, 유유상종)
1 - 1. 정의
유유상종(類類相從) 이라는 사자성어가 있습니다. 다들 아시다시피 같은 무리 안에서 서로 사귄다는 의미입니다. 영어에도 비슷한 표현이 있습니다. Birds of a feather flock together, 같은 깃털의 새들이 떼지어 다닌다는 의미이죠. 동서양 양측 문화권에서 속담이나 격언으로 포착될 만큼, 같은 특징을 짓는 무리들이 서로 사귀고 몰려 다니는 현상은 현실의 네트워크에서 흔히 관측되는 패턴입니다. 이를 네트워크의 assortativity (동류성) 이라고 합니다.
Assortativity가 발생하는 메커니즘은 두 가지로 나눠볼 수 있는데, 하나는 homophily (동종 선호)로, 자신과 비슷한 사람과 친해지거나 어울리게 되는 현상입니다. 다른 하나는 social influence로, 연결된 node들이 갈수록 비슷해지는 메커니즘입니다. 굳이 사자성어에서 찾아보면, 근묵자흑 정도가 있겠군요.
Assortativity는 자연스러운 현상입니다. 하지만 자연스러움과는 별개로 사회에 안 좋은 영향을 줄 수 있습니다. 대표적인 것이 echo chamber effect (반향실 효과)로, 비슷한 의견을 가진 사람끼리 지나치게 교류한 결과, 기존의 믿음과 의견이 더욱 강화되어 외부의 정보와 견해를 불신하게 되는 현상입니다. 이런 환경 하에서는 다양성이 소멸될 수 있고, 그룹 안에서의 아집이나 편견이 해소되지 않고 계속 강화될 수 있다는 문제점이 있습니다. 현대 사회의 SNS나 여러 커뮤니티 사이트에서 정보가 생성되어 그 안에서 퍼져나가는 현상을 바라보면, 네트워크의 assortativity가 얼마나 무서운 영향을 줄 수 있는지 느낄 수 있습니다.
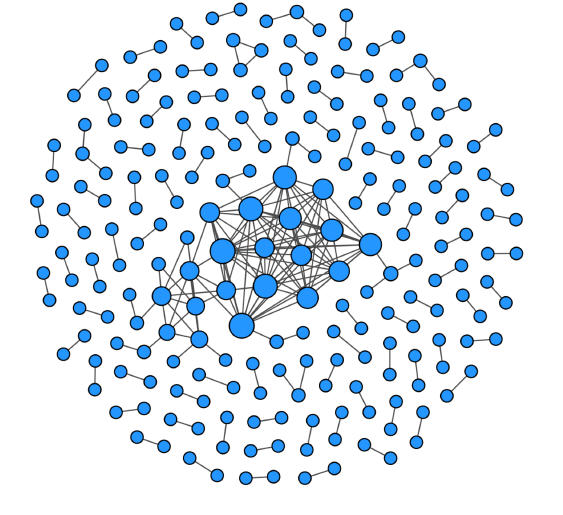
Assortative network의 특징은 hub가 중심부에 자리잡고 코어 (core) 와 주변부 (periphery) 의 구조를 갖는다는 것입니다. 즉, 중앙에 degree가 굉장히 큰, 또는 사회적 영향력이 큰 노드들이 자리 잡고, degree 낮은, 또는 사회적 영향력이 작은 노드들이 주변부에 있다는 것입니다. 대표적인 예시는 페이스북이나 트위터 등의 소셜네트워크 입니다.

Disassortative network는 다수의 별모양 구조 (star structure)를 가진다는 것이 특징입니다. 즉, 강한 영향력을 가진 hub가 다수 존재하고 그 hub들을 중점으로 다른 노드들이 별 모양의 형태로 연결되어 있습니다. 그리고 hub들은 보통 서로 연결되어 있지 않고 각각의 community를 형성합니다. 대표적인 예는 인터넷이나 webpage network 입니다.
1 - 2. Measurement
그렇다면 assortativity는 어떻게 측정할까요?
만약 node에 연관된 다른 변수들 (attributes) 이 존재하고, 우리가 네트워크에 관련된 사전지식이 있다면, 변수들을 이용하여 assortativity를 측정하는 것이 자연스러울 것입니다. 다행히도 networkx 라이브러리에 관련 매서드들이 존재합니다. 아래와 같이 node의 attribute가 categorical variable인 경우와 numeric variable인 경우로 매서드가 나뉘어져 있습니다.
import networkx as nx
## categorical variable
assort_category = nx.attribute_assortativity_coefficient(G, category)
## numeric variable
assort_numeric = nx.attribute_assortativity_coefficient(G, numeric)만약 node attribute가 존재하지 않는다면, degree를 이용하는 것이 자연스러울 것입니다. 이때 사용하는 것이 Pearson correlation coefficient로 다음과 같이 정의됩니다.
$$r = \frac{ \sum_{jk}jk\left( e_{jk} - q_{j}q_{k} \right) }{\sigma^{2}_{q}}$$
여기서, $q_{k} = \frac{(k+1)p_{k+1}}{\sum_{j \geq 1}jp_{j}}$는 remaining degree의 분포로, degree의 분포 $p_{k}$로부터 정의됩니다. Remaining degree는 네트워크의 임의의 edge를 따라 갔을 때 target node의 남은 degree라고 보시면 됩니다. 그리고 $e_{jk}$는 remaining degree의 joint probability distribution 입니다.
Pearson correlation coefficient는 -1과 1 사이의 값을 가지며 1에 가까울수록 네트워크의 assortativity가 크다는 것을 알 수 있습니다. Networkx 패키지에는 nx.degree_assortativity_coefficient(G) 매서드로 상관계수를 계산할 수 있습니다.
# Pearson correlation between degree of adjacent nodes
r = nx.degree_assortativity_coefficient(G)2. Small world
2 - 1. Path
(1) Path (경로): 두 노드 사이의 일련의 연결(edge)을 의미합니다. 즉, 두 노드를 연결하는 node의 sequence라고 볼 수 있습니다. Directed network의 경우, edge들의 방향성에 따라 연결되어야 합니다.
(2) Cycle: 시작 노드와 타겟 노드가 같은 path
(3) Simple path (단순 경로): 경로를 구성하는 모든 edge가 다른 path. 즉, 같은 edge를 2번 이상 지나치면 안 됩니다. 한붓 그리기가 대표적인 simple path 입니다.
(4) path length (경로의 길이): path를 구성하는 edge의 개수
(5) shortest path between two nodes: 두 노드 사이의 가장 짧은 path. (shortest path는 여러 개 있을 수도 있습니다.)
(6) shortest path length: shortest path의 length. 만약 path가 존재하지 않는다면 length는 무한대라고 생각합니다.
이제 networkx 패키지를 이용하여 다음과 같은 네트워크를 예로 들어봅시다.
G = nx.Graph()
G.add_nodes_from(['a','b','c','d','e','f','g','h','i'])
G.add_edges_from([('a','e'),('b','h'),('d','e'),('d','f'),('e','f'),('f','g'),('f','h'),('h', 'i')])
nx.draw(G, with_labels=True, node_size=1000)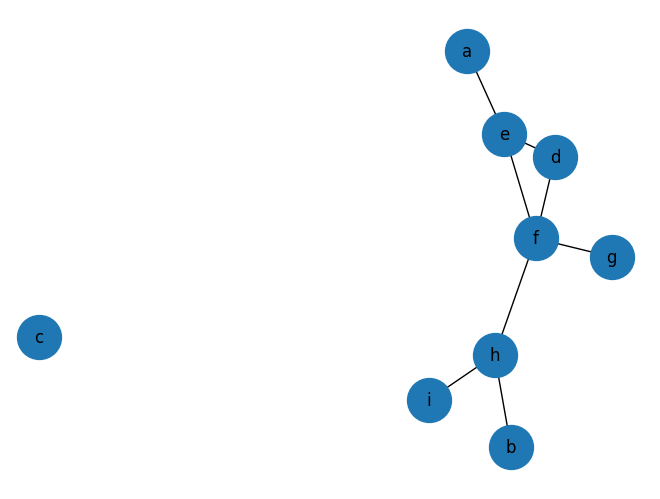
nx.has_path(G, node1, node2) 매서드는 node1과 node2 사이에 path가 존재하는지를 True 또는 False로 반환해줍니다. 위의 그림을 보면 알 수 있듯이 노드 a와 b 사이에는 path가 존재하지만, a와 c 사이에는 path가 존재하지 않습니다.
print(nx.has_path(G, 'a', 'c')) # False
print(nx.has_path(G, 'a', 'b')) # Truenx.shortest_path 매서드는 기본적으로 네트워크 G를 파라메터로 받습니다. 여기에 두 개의 node를 파라메터로 주면 두 노드 사이의 shortest path를 반환합니다. 위의 그림에서 노드 a와 b 사이의 shortest path는 a-e-f-h-b로 나타납니다. nx.shortest_path에 하나의 node를 주면 해당 노드로부터 각 노드로의 shortet path를 dictionary의 형태로 반환하고, 아무 node도 주지 않는다면, 모든 노드 쌍 (pair)의 shortest path를 반환합니다. nx.shortest_path_length도 비슷한 방식으로 작동하여 shortest path의 길이를 반환합니다.
print(nx.shortest_path(G, 'a', 'b')) # ['a','e','f',h','b']
print(nx.shortest_path_length(G,'a','b')) # 4
print(nx.shortest_path(G, 'a')) # dictionary
print(nx.shortest_path_length(G, 'a')) # dictionary
print(nx.shortest_path(G)) # all pairs
print(nx.shortest_path_length(G)) # all pairs
Shortest path가 중요한 이유는 shortest path들을 통해서 네트워크가 얼마나 조밀하게 연결되어 있는 지를 특징 지을 수 있기 때문입니다.
2 - 2. Diameter와 average path length (APL)
(1) Diameter: 네트워크에 존재하는 가장 긴 shortest path length로 다음과 같이 정의할 수 있습니다.
$$l_{max} =\underset{i, j}{\max} l_{ij}$$
(2) Average path length: 모든 node 쌍 (pair)에 대한 shortest path length들의 평균입니다.
Undirected network: $<l> = \frac{\sum_{i,j}l_{ij}}{\binom{N}{2}} = \frac{2 \sum_{i,j} l_{ij}}{N(N-1)}$
Directed network: $<l> = \frac{\sum_{i,j}l_{ij}}{N(N-1)}$
만약, 하나 또는 그 이상의 노드 쌍에 path가 존재하지 않는다면, diameter 또는 APL은 정의되지 않는다고 볼 수 있습니다. (networkx 패키지의 경우)
하지만, 대부분의 네트워크들은 연결되지 않는 node들이 존재합니다. 이 경우에도 diameter나 APL 값을 얻고 싶다면, 가장 큰 connected component (연결된 subnetwork)의 diameter나 APL을 사용할 수도 있고, 다음과 같은 수학적 트릭을 사용할 수도 있습니다.
$$<l> = \left( \frac{\sum_{i,j}{\frac{1}{l_{ij}}}}{\binom{N}{2}} \right)^{-1}$$
다시 위에서 예로 든 네트워크를 사용해봅시다. 이 네트워크는 노드 c의 존재로 인해 c가 포함된 노드 쌍에 대해서는 path가 존재하지 않습니다. 따라서 networkx 패키지의 nx.average_shortest_path_length() 매서드는 에러를 반환합니다.
하지만 아래 코드에서처럼 노드 c를 제거하면, APL을 구할 수 있습니다. 대략 2.143.이 나오는 것을 확인할 수 있습니다.

print(nx.average_shortest_path_length(G)) # error
G.remove_node('c') # make G connected
print(nx.average_shortest_path_length(G)) # now it works, 2.143이제 directed network에서의 path를 networkx를 통해 알아봅시다. 아래의 코드를 통해서 예시를 만들었습니다.
D = nx.DiGraph()
D.add_nodes_from(['a','b','c','d','e','f','g','h','i'])
D.add_edges_from([('a','e'),('h','b'),('e','d'),('d','f'),('f','e'),('f','g'),('f','h'),('i', 'h')])
nx.draw(D, with_labels=True, node_size=700)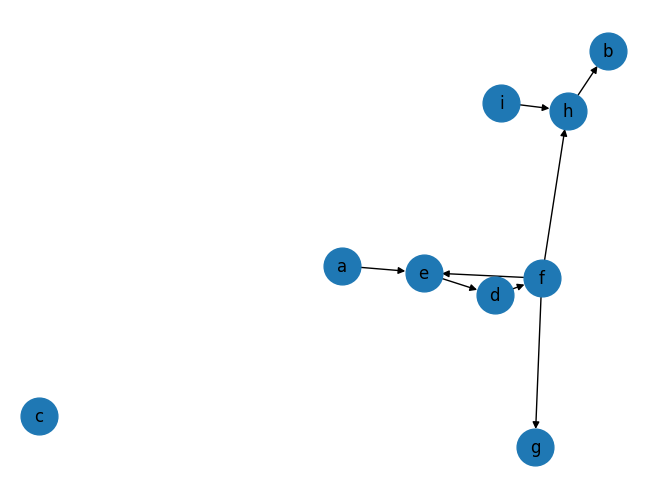
노드 a로부터 b로 가는 path는 존재하지만, 노드 b로부터 a로 가는 path는 존재하지 않음을 확인할 수 있습니다. 그리고 노드 a로 부터 b로 가는 shortest path도 출력해 보았습니다.
print(nx.has_path(D, 'b', 'a')) # False
print(nx.has_path(D, 'a', 'b')) # True
print(nx.shortest_path(D, 'a', 'b')) # ['a','e','d','f',h','b']마지막으로, weighted undirected network에서 path를 확인해봅시다.
아래의 코드를 이용해서 network을 생성하였습니다.
W = nx.Graph()
W.add_nodes_from(['a','b','c','d','e','f','g','h','i'])
W.add_weighted_edges_from([('a','e',2),('b','h',2),('d','e',1),('d','f',1),('e','f', 3),('f','g',2),('f','h',1),('h', 'i',1)])Weight이 있는 만큼, 시각화에 좀 더 신경을 써보았습니다. Edge에 weight가 labeling 되도록 했고, weight의 1.0을 기준으로 edge를 다른 색으로 시각화 하였습니다.
import matplotlib.pyplot as plt
elarge = [(u, v) for (u, v, d) in W.edges(data=True) if d["weight"] > 1.0]
esmall = [(u, v) for (u, v, d) in W.edges(data=True) if d["weight"] <= 1.0]
pos = nx.spring_layout(G, seed=7)
nx.draw_networkx_nodes(W, pos, node_size=700)
nx.draw_networkx_edges(W, pos, edgelist=elarge, width=6)
nx.draw_networkx_edges(W, pos, edgelist=esmall, width=6, alpha=0.5, edge_color="b", style="dashed"
)
nx.draw_networkx_labels(W, pos, font_size=20, font_family="sans-serif")
edge_labels = nx.get_edge_attributes(W, "weight")
nx.draw_networkx_edge_labels(W, pos, edge_labels)
ax = plt.gca()
ax.margins(0.08)
plt.axis("off")
plt.tight_layout()
plt.show()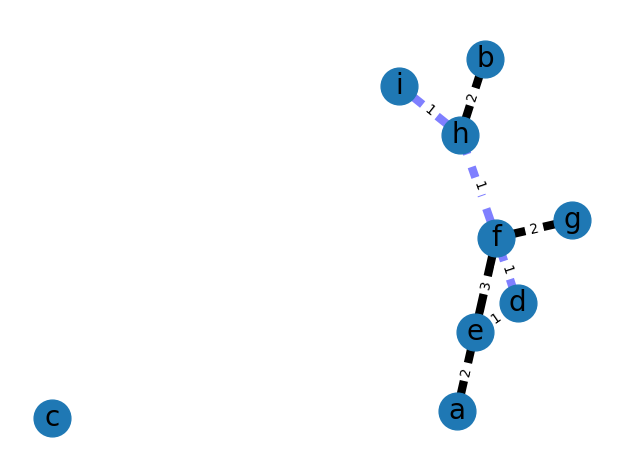
이제 nx.shortest_path_length를 통해서 노드 a와 b 사이의 shortest path length를 계산해봅니다. 주의할 점은 'weight' 파라매터를 주지 않으면 unwieghted의 경우로 shortest path를 준다는 점입니다. 'weight'를 파라매터로 주면, weight가 마치 거리처럼 적용 되어 shortest path가 계산 됩니다. 위의 예시의 경우, 'weight' 파라매터를 주지 않으면 노드 a와 b 사이의 shortest path는 a-e-f-h-b로 undirected의 경우와 같지만, 'weight' 파라매터를 주면 shortest path가 a-e-d-f-h-b로 바뀝니다. Weight을 고려할 경우, a-e-d-f-h-b의 경로는 거리가 7이지만, a-e-f-h-b의 경로는 거리가 8이기 때문입니다.
print(nx.shortest_path(W,'a','b')) # ['a', 'e', 'f', 'h', 'b']
print(nx.shortest_path_length(W, 'a', 'b')) # 4
print(nx.shortest_path(W,'a','b', 'weight')) # ['a', 'e', 'd', 'f', 'h', 'b']
print(nx.shortest_path_length(W, 'a', 'b', 'weight')) # 72 - 3. Connected network
(1) Connected network: 임의의 두 노드 사이에 path가 존재하는 네트워크.
(2) Disconnected network: connected하지 않은 네트워크. Disconnected network는 다수의 connected components로 구성됩니다.
(3) Connected component: connected subnetwork (연결된 부분 네트워크). 가장 큰 connected component를 giant component라고 하며, 보통 이러한 giant component는 네트워크의 상당히 많은 부분을 차지합니다.
(4) Singleton: 가장 작은 connected component로 다른 어떠한 노드와도 연결 되어있지 않은 섬과 같은 node를 말합니다.
아래의 예시를 통해 각 개념들을 살펴봅시다.
G = nx.Graph()
G.add_nodes_from(['a','b','c','d','e','f','g','h','i','j','k'])
G.add_edges_from([('a','b'),('b','c'),('b','d'),('c','d'),('d','e'),('d','f'),('f','g'),('f', 'h'),('j', 'k')])
pos = nx.spring_layout(G, seed=7)
nx.draw(G, pos, with_labels=True, node_size=700)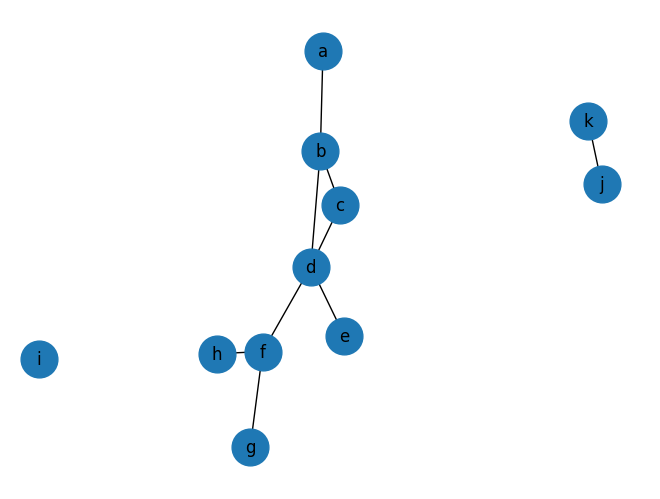
nx.is_connected() 매서드를 통해 위의 네트워크가 disconnected network임을 확인할 수 있습니다.
nx.connected_components()는 네트워크의 connected component들을 반환합니다. 보통 giant component가 주 분석 대상이기 때문에 sort를 할 때는 내림차순으로 해줍니다. 위의 예시에서 giant component를 구성하는 노드는 a,b,c,d,e,f,g 임을 확인 할 수 있습니다.
nx.subgraph는 주어진 node들로 생성되는 subgraph를 반환합니다. 이를 통해 giant component만을 따로 떼서 분석할 수 있습니다. 당연히 giant component는 connected network임을 맨 아래의 라인을 통해 확인할 수 있습니다.
print(nx.is_connected(G)) # False
comps = sorted(nx.connected_components(G), key=len, reverse=True)
print(comps) #[{'g', 'c', 'a', 'h', 'b', 'e', 'd', 'f'}, {'k', 'j'}, {'i'}]
nodes_in_giant_comp = comps[0]
print(nodes_in_giant_comp) # {'g', 'c', 'a', 'h', 'b', 'e', 'd', 'f'}
GC = nx.subgraph(G, nodes_in_giant_comp)
print(nx.is_connected(GC)) # True
Directed network의 경우, connectedness는 두 가지가 존재합니다.
Strongly connected network: 모든 노드 쌍에 대하여 path가 존재하는 네트워크
Weakly connected network: Edge의 방향성을 고려하지 않고, 모든 노드 쌍에 대하여 path가 존재하는 네트워크
같은 방식으로 strongly connected component 와 weakly connected component가 정의됩니다.
이외에도 in-component 와 out-component라는 것이 존재합니다.
in-component of stronly connected component S: S의 노드로 가는 path는 존재하지만, S의 노드들로부터는 도달 불가능한 노드들의 집합.
out-component of strongly connected component S: S의 노드들로부터 도달 가능하지만, S의 노드로 가는 path는 존재하지 않는 노드들의 집합.
글로만 보면 헷갈리니 예시를 들어 살펴봅시다. 아래의 코드로 directed network를 생성하고, 보기 쉽게 노드별로 색을 지정해주었습니다.
D = nx.DiGraph()
D.add_nodes_from(['a','b','c','d','e','f','g','h','i','j','k'])
D.add_edges_from([('a','b'),('b','c'),('d','b'),('c','d'),('d','e'),('d','f'),('f','g'),('h', 'f'),('k', 'j')])
pos = nx.spring_layout(G, seed=7)
color_map = []
for node in D:
if node in ['b', 'c', 'd']:
color_map.append('blue')
elif node in ['j', 'k']:
color_map.append('red')
elif node in ['i']:
color_map.append('yellow')
elif node in ['a']:
color_map.append('green')
elif node in ['e', 'f', 'g']:
color_map.append('orange')
else:
color_map.append('purple')
nx.draw(D, pos, with_labels=True, node_size=700, node_color=color_map)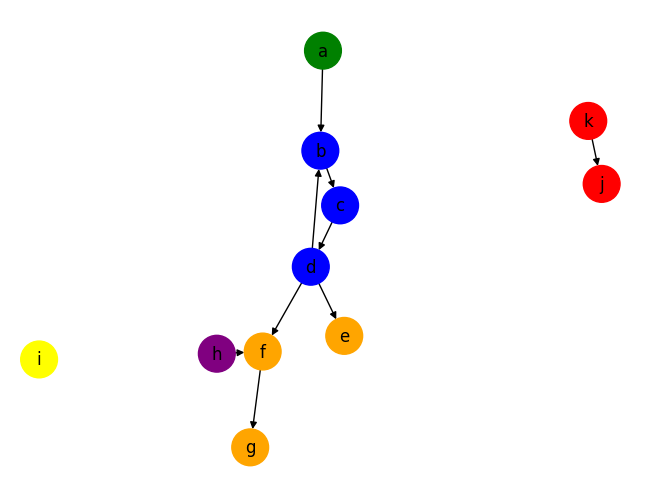
is_strongly_connected()와 is_weakly_connected()를 통해 위의 네트워크가 strongly and weakly connected 하지 않음을 확인할 수 있습니다.
weakly_connected_components() 매서드를 사용하면 위의 네트워크가 3개의 components로 구성됨을 알 수 있습니다.
반면에 strongly_connected_components()를 사용하면, 위의 네트워크는 가운데의 파란색 노드들 {b,c,d}를 제외하고는 모두 singleton들로 구성됨을 알 수 있습니다.
Strongly connected component {b,c,d}를 기준으로 in-component는 초록색 node인 {a} 입니다. 그리고 out-component는 주황색 노드들의 집합인 {e,f,g} 입니다.
print(nx.is_strongly_connected(D)) # False
print(nx.is_weakly_connected(D)) # False
print(list(nx.weakly_connected_components(D))) # [{'g', 'c', 'a', 'h', 'b', 'e', 'd', 'f'}, {'i'}, {'k', 'j'}]
print(list(nx.strongly_connected_components(D))) # lots of singletons2 - 4. Trees
이산수학이나 자료 구조에서 자주 등장하는 tree 구조 또한 network의 한 종류입니다. Tree는 다음과 같이 정의됩니다.
Def) A tree is a connected network without cycles.
즉, connected 네트워크면서 동시에 cycle이 없는 네트워크가 바로 tree 입니다.
Tree는 다음과 같은 특징을 같습니다.
(1) A tree is a connected network with N-1 edges.
사실, 이 특징과 tree의 정의는 equivalent 합니다.
(2) 또한, tree의 경우, 두 노드 사이의 경로는 단 하나로 유일합니다.
(3) Tree는 서열이 존재하는 network로 root를 제외한 각 노드는 하나의 parent node (부모 노드)와 다수의 child nodes (자식 노드)와 연결되어있습니다 (leaf node 제외).
아래의 코드를 통해 대표적인 네트워크들 (cycle, star, path, complete) 을 생성하였습니다.
C = nx.cycle_graph(4)
S = nx.star_graph(5)
P = nx.path_graph(5)
K = nx.complete_graph(5)
plt.subplot(221)
nx.draw(C)
plt.subplot(222)
nx.draw(S,node_color='k')
plt.subplot(223)
nx.draw(P,node_color='g')
plt.subplot(224)
nx.draw(K,node_color='b')
plt.show()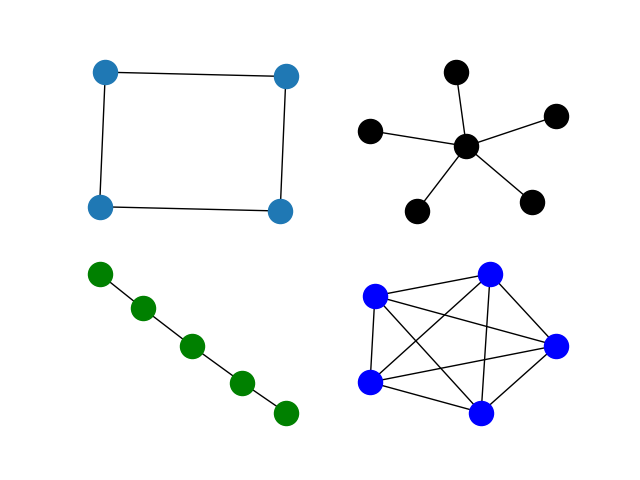
이제 nx.is_tree() 매서드를 통해 해당 네트워크가 tree인지를 확인할 수 있습니다.
당연하게도, cycle graph는 말 그대로 cycle 그 자체 이므로 tree가 아니며, complete graph는 모든 node가 서로 연결되어 있으므로, cycle이 존재하기 때문에 tree가 아닙니다. 반면에 star graph는 root 노드를 제외한 노든 노드들이 root 노드의 자식 노드인 극단적인 형태의 tree이며, path graph는 root로부터 leaf까지 일렬로 나열된 형태의 극단적인 형태의 tree 입니다.
print(nx.is_tree(C)) # False
print(nx.is_tree(S)) # True
print(nx.is_tree(P)) # True
print(nx.is_tree(K)) # False2 - 5. Small world
실제 social network는 small world의 형태를 가집니다. 즉, 노드들 간의 shortest path의 길이는 우리들의 예상과 다릴 의외로 짧습니다. 대표적으로, Stanley Milgram의 실험을 통해 평균적인 social distance 가 6.5 step 정도임이 밝혀졌습니다. 임의의 사람이 6 명 정도만 거치면 나와 연결된다는 것입니다.
그렇다면 path가 "짧다"는 것은 얼마나 짧아야하는 것일까요?
Path가 짧다는 것은 네트워크의 크기에 따라 다릅니다. 보통 APL이 짧다고 하는 경우는 네트워크의 크기 $N$에 대해서 매우 느리게 APL이 증가하는 경우입니다. 예를 들면, $log$ scale로 말이죠. $<l> \sim logN$
3. Friend of friend (친구의 친구)
이 포스트에서 다룰 마지막 현실의 네트워크 데이터의 특성은 fiend of friend 입니다. 친구의 친구는 곧 내 친구라는 의미죠. 이러한 특성은 특히 페이스북이나 인스타그램 등의 SNS 네트워크에서 자주 나타납니다. 네트워크에서 친구의 친구는 3개의 노드가 서로 연결된 triangle (삼각형)의 형태로 나타납니다. 즉, 현실 네트워크 데이터의 특징은 이러한 삼각형이 굉장히 많이 관찰된다는 것입니다. Directed network의 경우에는 다양한 형태의 삼각형이 나타날 수 있기 때문에 분석할 삼각형의 형태를 고정 시켜야 합니다.
3 - 1. Clustering coefficient
주어진 노드가 포함된 실제 삼각형의 개수와 주어진 노드가 포함될 수 있는 최대의 삼각형의 개수를 비교해서 노드의 clustering coefficient를 계산할 수 있습니다.
$$C(i) = \frac{\tau(i)}{\tau_{max}(i)} = \frac{\tau(i)}{\binom{k_{i}}{2}}=\frac{2\tau(i)}{k_{i}(k_{i}-1)}$$
여기서 $\tau(i)$는 노드 $i$가 포함된 삼각형의 개수이며, $k_{i}$는 노드 $i$의 degree 입니다.
주의할 점은 clustering coefficient가 $k_{i} \geq 2$일 때만 정의가 가능하다는 점입니다. 하지만 networkx 패키지에서는 $k_{i}=0$ 또는 $k_{i}=1$인 경우, clustering coefficient를 0으로 줍니다.
네트워크 $G$의 clustering coefficient는 각 노드의 clustering coefficient의 평균으로 정의할 수 있습니다.
$$C = \frac{\sum_{i:k_{i}>1} C(i)}{N_{k>1}}$$
이 경우, singleton node와 degree가 1인 node들은 계산에서 제외되어야 합니다. 하지만 networkx는 해당 node들의 clustering coefficient를 0으로 놓고 계산에 포함합니다.
이제 아래의 코드로 생성된 네트워크를 예시로 clustering coefficient를 계산해 봅시다.
G = nx.Graph()
G.add_nodes_from(['a','b','c','d','e','f','g','h'])
G.add_edges_from([('a','g'),('a','f'),('b','c'),('b','e'),('b','g'),('b','h'),('c','g'),('c', 'e'),('d', 'e')])
pos = nx.spring_layout(G, seed=7)
nx.draw(G, pos, with_labels=True, node_size=700)
nx.triangles(G) 는 네트워크 G의 triangle의 개수를 dictionary의 형태로 반환합니다. (key: node)
nx.clustering() 매서드는 노드를 파라매터로 주면, 해당 노드의 clustering coefficient를 계산합니다.
노드 d의 경우, 사실 clustering coefficient가 정의 되지 않지만, networkx에서는 0의 값을 주는 것을 확인할 수 있습니다.
또한 노드 b의 경우, $\frac{2}{\binom{4}{2}} = \frac{1}{3}=0.3333$ 임을 확인할 수 있습니다.
nx.clustering() 매서드에 노드 파라매터를 명시하지 않으면, 각 노드의 clustering coefficient를 dictionary의 형태로 반환합니다.
마지막으로, nx.average_clustering() 매서드는 네트워크 전체의 clustering coefficient를 계산합니다.
print(nx.triangles(G)) # {'a': 0, 'b': 2, 'c': 2, 'd': 0, 'e': 1, 'f': 0, 'g': 1, 'h': 0}
print(nx.clustering(G,'b')) # 0.3333
print(nx.clustering(G, 'd')) # 0
print(nx.clustering(G)) # dict node -> clustering coefficient
print(nx.average_clustering(G)) # 0.20833333333333331'데이터 사이언스' 카테고리의 다른 글
| 네트워크 데이터 분석 - robustness, core decomposition, assortativity (1) | 2024.07.01 |
|---|---|
| 네트워크 데이터 분석 - Centrality (0) | 2024.06.29 |
| 네트워크 데이터 분석 - Networkx (0) | 2024.06.24 |
| 네트워크 데이터 분석 - 서론 (0) | 2024.06.20 |
| Bootstrap으로 신뢰구간 구하기 (1) | 2024.06.18 |
 Skypainter
Skypainter