목차
이번 포스트에스는 노드의 구심성 (centrality) 에 대해서 다뤄보겠습니다.
1. What is it?
현실 네트워크의 특징중 하나는 모든 노드나 edge가 같은 중요성을 갖지 않는다는 것입니다. 특정 노드 또는 edge는 네트워크에서 더욱 중요한 위치를 차지하고 있죠. 예를 들어, 친구 네트워크의 경우, 굉장히 E인 (또는 인싸인) 친구가 네트워크에서 중추적인 역할을 차지하고 있는 경우를 많이 볼 수 있습니다. 그 친구를 중심으로 여러 친구들이 모이고, 그 친구를 통해서 내가 잘 모르는 다른 친구들의 이야기도 들을 수 있죠. 이러한 친구 또는 노드를 central 하다고 합니다.
하지만 노드의 centrality는 또 다른 관점으로 생각할 수도 있습니다. 어떤 노드가 네트워크 전체적으로 볼 때 중요한 다리 역할을 하는 경우도 생각해볼 수 있습니다. 예를 들어, 어떤 정치 네트워크를 생각해봅시다. 이 네트워크는 크게 두 그룹으로 구성 되어 있는데 하나는 보수 정당, 다른 하나는 진보 정당이라고 하죠. 이때 제 3지대에서 중립적인 정치인이 나타났다고 생각합시다. 그리고 이 정치인이 캐스팅 보트를 쥐고 있기 때문에 각 당의 대표가 이 정치인을 자주 만난다고 하면, 이 중립적인 정치인이 네트워크 전체에 끼치는 영향은 꽤 클 것입니다. 왜냐하면 이 정치인이 대립하는 두 정당을 중재하고, 의사 소통의 다리 역할을 할 수도 있기 때문이죠. 이런 경우, 중립적인 정치인은 단 2명의 정치인과 연결 되어있지만, 네트워크에서 아주 중요한 역할을 하므로 centrality가 높다고 할 수 있습니다.
2. How to measure?
그렇다면 centrality는 어떻게 측정할까요?
Centrality는 다양하게 정의될 수 있기 때문에 measurement 또한 다양합니다. 이 포스트에서는 대표적인 4 가지를 다루겠습니다.
2 - 1. Degree
가장 먼저 떠오르는 centrality의 측정 방법은 바로 degree일 것입니다. Degree란 해당 노드와 인접한 노드의 개수이기 때문에 degree가 클수록 영향력이 큰 노드라고 볼 수 있습니다. 이렇게 큰 degree를 가지는 노드를 hub 라고 부릅니다.
2 - 2. Closeness
노드가 중요할수록 다른 노드와의 거리가 평균적으로 가까울 것입니다. 이 아이디어를 반영한 centrality의 측도가 바로 closeness 입니다. 구체적으로, closeness는 다음과 같이 정의 됩니다.
$$g_{i} = \frac{N-1}{\sum_{i \neq j} l_{ij}}$$
여기서 $N$은 네트워크의 노드 개수이고, $l_{ij}$는 노드 $i$와 $j$ 사이의 거리입니다. (length of the shortest path)
Networkx 패키지에서는 nx.closeness_centrality(G) 매서드를 이용해서 각 node의 closeness 값을 얻을 수 있습니다.
import networkx as nx
G = nx.Graph()
G.add_nodes_from(['a','b','c','d'])
G.add_edges_from([('a','b'),('a','c'),('b','c'),('c','d')])
pos = nx.spring_layout(G, seed=7)
nx.draw(G, pos, with_labels=True, node_size=700)
print(nx.closeness_centrality(G)) # {'a': 0.75, 'b': 0.75, 'c': 1.0, 'd': 0.6}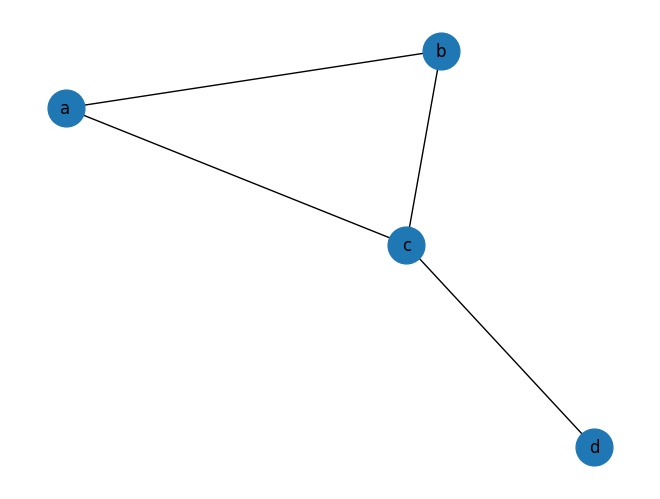
예시로 노드 b의 closeness를 계산해보면 다음과 같겠죠.
$$\text{closeness(b)} = \frac{N-1}{l_{a,b} + l_{b,c} + l_{b,d}} = \frac{4-1}{1+1+2} = 0.75$$
2 - 3. Betweenness
중요한 노드들은 정보가 전달 되는 경로들이 자주 지나가는 노드들일 것입니다. 이 아이디어를 반영한 centrality의 측도가 바로 betweenness 이며, 다음과 같이 정의 됩니다.
$$b_{i} = \sum_{i \neq h \neq j} \frac{\sigma_{hj} (i)}{\sigma_{hj}}$$
여기서 $\sigma_{hj}$는 노드 $h$에서 $j$로 가는 shortest path의 개수이며, $\sigma_{hj} (i)$는 노드 $h$에서 $j$로 가는 shortest path중 노드 $i$를 지나는 shortest path의 개수입니다.

간단하게 위 그림의 path network로 예를 들어 봅시다. Path network는 tree이기 때문에 모든 $i,j$에 대해 $\sigma_{ij}=1$ 입니다. 양 끝에 있는 노드 $a$와 $e$는 모든 shortest path가 지나가지 않으므로, betweenness가 0 이지만, 가운데에 있는 노드 $c$의 경우, $a$ → $d$, $a$ → $e$, $b$ → $d$, $b$ → $e$ 4개의 shortest path가 지나가므로, betweenness가 4가 됩니다.
| node | betweenness |
| a | 0 |
| b | 3 |
| c | 4 |
| d | 3 |
| e | 0 |
Hub들은 주로 높은 값의 betweenness를 갖습니다. 하지만 hub가 아님에도 높은 betweenness 값을 가지는 노드들이 존재합니다. 아래의 네트워크에서는 노드 $e$가 그러한데, 두 그룹 {a,b,c,d}와 {f,g,h,i}를 잇는 다리 역할을 하기 때문이다. 이 경우, 한 그룹에서 발생한 정보는 반드시 노드 $e$를 거쳐야만 가른 그룹으로 전달될 수 있습니다.

Betweenness는 또한 node뿐만 아니라 edge에도 적용될 수 있습니다.
Edge betweenness: 모든 쌍의 node에 대한 shortest path의 개수와 해당 edge를 지나는 shortest path의 비율
Networkx에는 두 종류의 betweenness가 모두 구현 되어있습니다. nx.betweenness_centrality() 매서드는 dictionary의 형태로 각 노드의 betweenness를 반환하고, nx.edge_betweenness_centrality() 매서드는 dictionary의 형태로 각 edge의 betweenness를 반환합니다.
위의 네트워크에 적용해보니 노드 $d$와 $f$의 betweenness는 0.5357이고, 노드 $e$의 betweenness는 0.5714가 나옵니다. 노드 e의 degree는 2로, 가장 degree가 가장 작지만, betweenness는 가장 큰 값을 가짐을 확인할 수 있습니다.
print(nx.betweenness_centrality(G)) # dict nodes: betweenness
print(nx.edge_betweenness_centrality(G)) # dict links: betweenness2 - 4. Eigenvector - page rank
Centrality의 마지막 측도는 구글이 웹페이지의 랭킹을 계산할 때 사용하는 page rank 입니다. Page rank는 내가 누구와 연결되어 있느냐가 핵심입니다. 내가 인기가 많은 사람과 연결 되어 있는 경우가 인기가 그저그런 사람과 연결 되어 있는 경우보다 page rank 값이 높습니다.
Page rank는 네트워크 위에서의 랜덤워크에 기반합니다.
(1) 먼저, walker는 랜덤한 노드에서 시작합니다.
(2) 각 스텝마다 walker는 $\alpha$의 확률로 랜덤하게 현재 있는 노드에 연결된 edge를 따라 이동합니다. 또는 $1-\alpha$의 확률로 다른 노드로 jump 합니다. 이때 $\alpha$를 damping factor 라고 부릅니다.
(2)의 스텝을 무한번 반복할 때 walker가 노드 $i$에 위치했을 확률이 바로 page rank 입니다. 이는 다음의 식으로 계산할 수 있습니다.
$$\xi = \alpha A \xi + (1-\alpha)v$$
여기서 $A$는 column-normalized adjacency matrix입니다. (즉, 각 열의 합이 1이 되도록 normalized된 adjacency matrix 입니다.) $\alpha$는 damping factor로 0과 1 사이의 값을 가지고, $v$는 모든 element가 $1/N$인 열벡터 입니다.
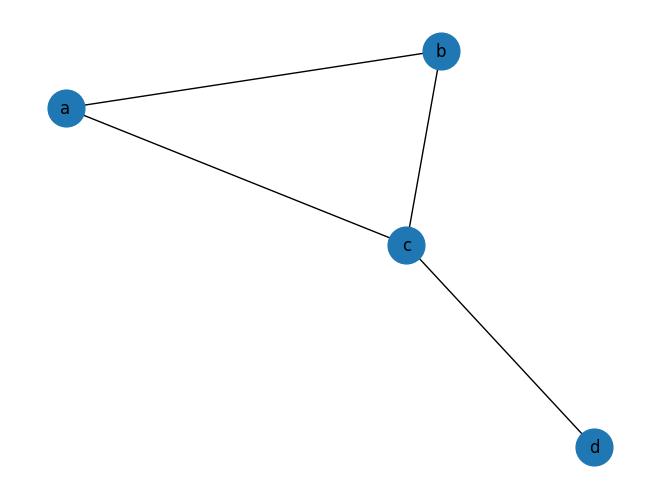
위의 네트워크를 예로 들면 $A$와 $v$는 다음과 같겠죠.
$$ A =\left( \begin{array}{cccc} 0 & 1/2 & 1/3 & 0 \\
1/2 & 0 & 1/3 & 0 \\
1/2 & 1/2 & 0 & 1 \\
0 & 0 & 1/3 & 0 \end{array} \right) $$
$$v = \begin{pmatrix}
1/4 \\
1/4 \\
1/4 \\
1/4
\end{pmatrix}$$
노드 $i$의 page rank 값은 dominant한 eigenvalue의 eigenvector의 $i$번째 entry 값이 됩니다. 그래서 page rank를 eigenvector centrality 라고도 부릅니다.
Networkx에서는 nx.pagerank() 라는 매서드로 구현이 되어있습니다.
nx.pagerank(G,alpha=0.85, max_iter=100)
이제 위의 모든 centrality measure들을 연 모양의 네트워크에 적용하여 값을 비교해봅시다.
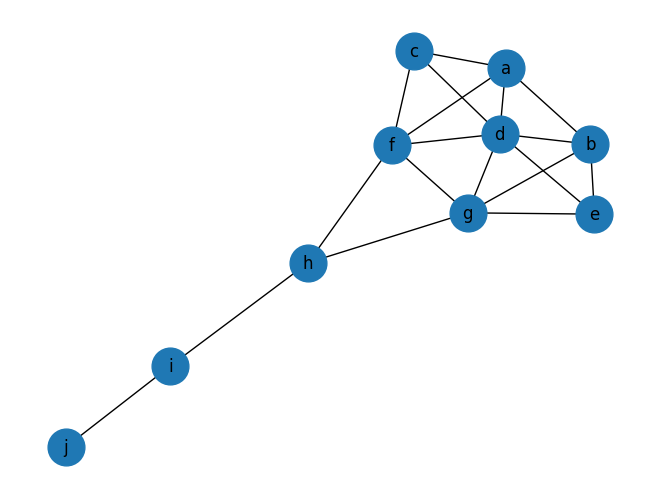
| node | degree | closeness | betweenness | page rank |
| a | 0.444 | 0.529 | 0.023 | 0.102 |
| b | 0.444 | 0.529 | 0.023 | 0.102 |
| c | 0.333 | 0.500 | 0.000 | 0.079 |
| d | 0.667 | 0.600 | 0.102 | 0.147 |
| e | 0.333 | 0.500 | 0.000 | 0.079 |
| f | 0.556 | 0.643 | 0.231 | 0.129 |
| g | 0.556 | 0.643 | 0.231 | 0.129 |
| h | 0.333 | 0.600 | 0.389 | 0.095 |
| i | 0.222 | 0.429 | 0.222 | 0.086 |
| j | 0.111 | 0.310 | 0.000 | 0.051 |
파란색은 각 centrality에서 가장 높은 값이고, 빨간색은 가장 작은 값입니다. 보시는 바와 같이 어떤 centrality를 사용하느냐에 따라 결과가 많이 달라지는 것을 확인할 수 있습니다.
결론적으로, degree는 노드가 popular한 정도를, closeness는 정보가 확산하는 경로에서 얼마나 잘 위치해 있는가를, betweenness는 노드가 네트워크에서 차지하고 있는 독보적인 브로커 혹은 다리 역할을, page rank는 얼마나 인기가 많은 친구를 두고 있는가를 바탕으로 노드의 중요도를 계산한다고 정리할 수 있겠습니다.
3. Centrality distribution
작은 네트워크에서는 어떤 노드가 중요한지 각각 판별하는 것이 의미 있는 일일 수도 있으나, 거대한 네트워크에서는 이런 작업이 큰 의미를 가지지 못 합니다. 이러한 경우, 통계적인 접근이 필요합니다. 비슷한 정도의 centrality를 가지는 노드를 묶어서 보거나, centrality의 분포를 볼 수 있다면, 네트워크의 특징을 파악하는 데에 도움이 되기 때문입니다.
3 - 1. Degree distribution
정수 값을 갖는 degree의 경우, 이산 확률 분포를 이용하면 됩니다.
$$f_{k} = \frac{n_{k}}{N}$$
$n_{k}$: degree가 k인 노드의 개수
email-enron-only 라는 데이터를 사용해서 degree distribution을 그려보겠습니다.
이 네트워크는 Enron 사의 이메일 커뮤니케이션에 대한 정보를 담고 있습니다.
(다운로드 링크: https://networkrepository.com/email.php)
Email Networks | Network Data Repository
email network data sets, email networks, email communications, email graphs, dynamic networks, temporal graphs, download email network data, network data, network data sets, graph data, download graph data, download network data, graph data sets, graph dat
networkrepository.com
파일 형식이 mtx이기 때문에 scipy의 mmread를 이용해서 먼저 데이터를 읽어줘야 합니다.
네트워크를 그려보면, 노드가 100 개 이상인 복잡한 네트워크임을 확인할 수 있습니다.
from scipy.io import mmread
data = mmread('email-enron-only.mtx')
G = nx.Graph(data, nodetype=int)
nx.draw(G)
max의 key 파라매터를 이용하면 쉽게 가장 degree가 큰 노드를 확인할 수 있습니다. 104번 노드가 42의 degree를 갖습니다.
highest_degree_node = max(G.nodes, key=G.degree)
print(highest_degree_node) ## 104
print(G.degree(highest_degree_node)) ## 42이제 degree distribution을 그려봅시다. Counter()를 이용해서 각 degree의 빈도를 계산합니다. 보통 degree의 확률값은 0에 가까운 값들이 많기 때문에 log scale을 이용해서 plot을 그려줬습니다.
from collections import Counter
import matplotlib.pyplot as plt
import numpy as np
degree_sequence = [G.degree(n) for n in G.nodes]
degree_counts = Counter(degree_sequence)
min_degree, max_degree = min(degree_counts.keys()), max(degree_counts.keys())
N = nx.number_of_nodes(G)
plot_x = list(range(min_degree, max_degree + 1))
plot_y = [degree_counts.get(x, 0) / N for x in plot_x]
fig, ax = plt.subplots()
#ax.set_xscale('log', base=10)
ax.set_yscale('log', base=10)
ax.plot(plot_x, plot_y)
plt.show()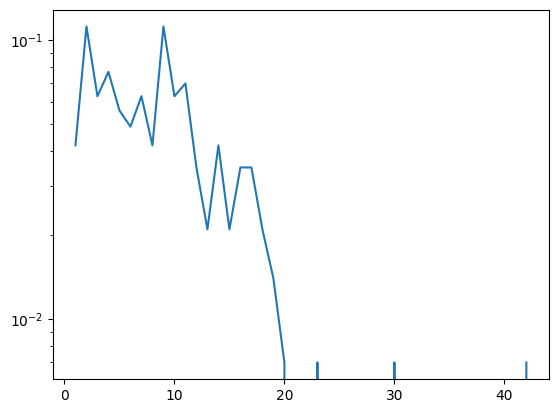
이 데이터는 노드의 개수가 엄청나게 많지는 않으므로, 히스토그램도 한번 그려보았습니다.
plot_x = list(range(min_degree, max_degree + 1))
plot_y = [degree_counts.get(x, 0) for x in plot_x]
plt.bar(plot_x, plot_y)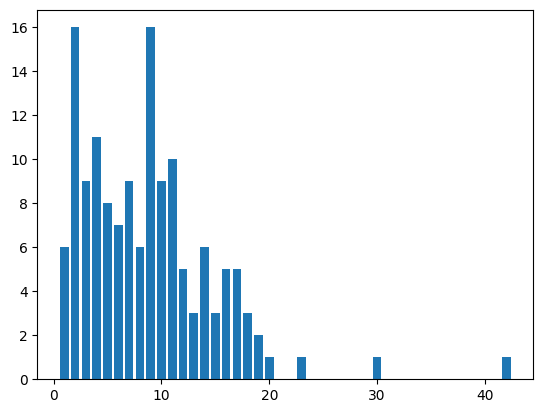
3 - 2. Heterogeniety parameter $\kappa$
Heterogeniety parameter $\kappa$는 네트워크가 얼마나 넓은 분포를 가지고 있는지를 계산합니다.
$$\kappa = \frac{<k^{2}>}{<k>^{2}}$$
여기서 $<k> = \frac{\sum_{i}l_{i}}{N}=\frac{2L}{N}$으로, 네트워크의 평균 degree이며, $<k^{2}> = \frac{\sum_{i}k_{i}^{2}}{N}$ 입니다.
만약 대부분의 노드의 degree가 $k_0$라는 값이라면, $<k> \approx k_{0}$ 하고, $<k^{2}> \approx k_{0}^{2}$일 것입니다. 따라서 $\kappa \approx 1$ 이 됩니다. 만약 분포의 $\kappa$가 1보다 아주 크다면, 분포가 heterogenous 하다고 합니다.
우리의 데이터의 $\kappa$는 약 1.48로 아주 heterogenous 하다고는 볼 수 없겠군요.
N = nx.number_of_nodes(G)
avg_degree = 2 * nx.number_of_edges(G) / N
avg_degree_squared = sum(np.square(degree_sequence)) / N
kappa = avg_degree_squared / np.square(avg_degree)
print(round(kappa, 2)) ## 1.483 - 3. Betweenness distribution
만약 betweenness처럼 centrality가 연속적인 값을 갖는 경우는 누적분포 (cumulative distribution)를 이용하면 됩니다.
$$P(x) = \sum_{v \geq x} f_{v}$$
$f_{v}$: $v$ 값을 갖는 노드의 빈도(frequency)
Betweenness 가 가장 높은 노드는 degree의 경우와 마찬가지로 104번 노드입니다. 그 값은 0.194 정도군요.
betweenness = nx.centrality.betweenness_centrality(G)
highest_betweenness_node = max(G.nodes, key=betweenness.get)
print(highest_betweenness_node) ## 104
print(betweenness[highest_betweenness_node]) ## 0.194아래의 코드는 betweenness의 cumulative distribution을 그려줍니다. 30개의 bin을 사용하여 빈도값들을 구하고 누적 확률을 구하였습니다. Degree와 마찬가지로, betweenness 또한 heavy tail을 가집니다.
betweenness = nx.centrality.betweenness_centrality(G)
betweenness_sequence = list(betweenness.values())
values, base = np.histogram(betweenness_sequence, bins=30)
N = nx.number_of_nodes(G)
cumulative = np.cumsum(values) / N
plt.plot(base[:-1], 1 - cumulative, c='blue')
plt.show()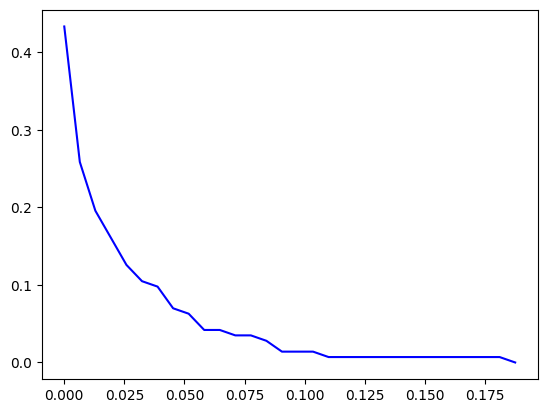
마지막으로 40개의 빈으로 히스토그램을 그려봤습니다.
counts, bins, patches = plt.hist(betweenness_sequence, bins=40)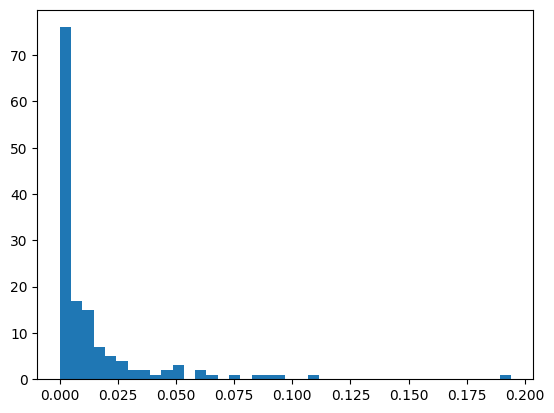
3 - 4. Friendship paradox
아래의 네트워크에서 노드를 랜덤으로 고른다면, 유비가 뽑힐 확률은 다른 인물들이 뽑힐 확률과 같습니다. 그러나 edge를 랜덤으로 뽑는다면 유비가 뽑힐 확률이 다른 인물들이 뽑힐 확률보다 높을 것입니다.
실제로 이 네트워크의 평균 degree는 2.29 입니다. 반면에, 이웃 노드의 degree의 평균은 2.83으로 평균 degree보다 큽니다. 이 숫자들이 의미하는 바는 평균적으로 내 친구들이 나보다 친구가 더 많다는 것입니다. 이를 friendship paradox 라고 합니다.
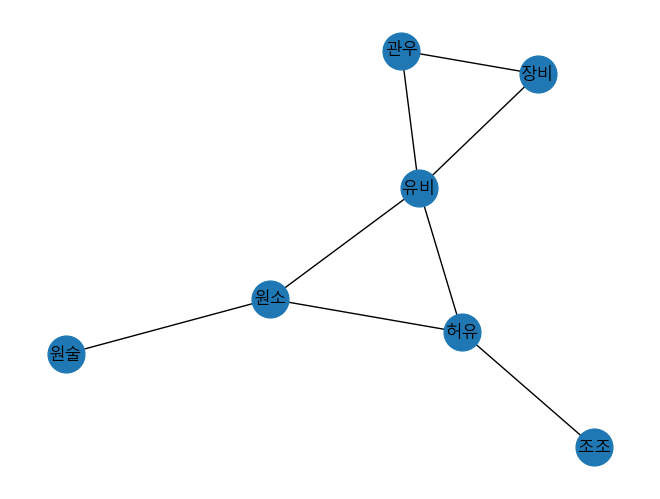
Friendship paradox가 발생하는 이유는 degree의 평균을 구할 때는 우리가 노드를 랜덤하게 선택하지만, 친구의 degree의 평균을 계산할 때는 우리는 연결된 edge에 따라 선택을 합니다. 따라서 친구가 $k$명 있는 사람은 $k$번 counting이 되어 평균값을 증가시킵니다. Hub가 많을수록 이러한 증가 효과는 더욱 커집니다.
 Skypainter
Skypainter