네트워크 데이터 분석 - robustness, core decomposition, assortativity

목차

 

이번 포스트에서는 네트워크의 robustness (강건성), core decomposition 그리고 네트워크에 그룹이 2개 있는 경우에 정의가 가능한 heterophilicity (이호성)과 dyadicity (이극성)에 대해 다뤄 보겠습니다.

1. Robustness (강건성)

보통 시스템이 robust 하다고 하면, 시스템의 일부분이 작동하지 않아도 전체의 기능에 영향을 주지 않는 경우를 말합니다.
네트워크에서도 비슷하게 robustness를 정의할 수 있습니다. 노드나 edge를 제거할 때 전체 네트워크 구조가 어떻게 변하는지 보면 됩니다. 그러므로, 네트워크의 robustness의 키포인트는 connectedness (연결성) 이라고 볼 수 있습니다.

네트워크의 Robustness test는 0개의 노드에서부터 시작해서 모든 노드를 없애 가면서 네트워크 전체의 connectedness가 어떻게 변하는지 확인하는 작업입니다.
(1) 먼저 connected 네트워크를 가정합니다. 그리고 $S = \frac{\text{가장 큰 connected componet의 노드 개수}}{N}$ 라고 합시다. 그러면 가장 처음 $S=1$ 입니다. 
(2) 이제 노드를 하나씩 지우며 $S$의 plot을 그립니다. 노드를 지울수록 네트워크는 조각나고, $S$ 값은 0에 가까워질 것입니다.

그렇다면 robustness test를 수행할 때 노드는 어떤 방식으로 지워야 할까요?
두 가지 전략을 생각해볼 수 있습니다.
(1) random failure: 노드를 랜덤하게 지웁니다.
(2) attacks: 허브를 먼저 공격합니다. 즉, degree가 높은 노드일수록 지워질 확률이 큽니다.

지난 포스트에서 사용한 Enron 사의 이메일 데이터를 이용해서 robustness test를 해봅시다.

(네트워크 데이터 분석 - Centrality)

네트워크 데이터 분석 - Centrality

 

데이터로 네트워크를 생성하고, nx.connected_components()를 통해서 connected components의 리스트를 얻어보면, 단 하나의 connected component만이 존재한다는 것을 알 수 있습니다. 즉, 이 네트워크는 connected 하며, 네트워크의 core는 곧 전체 네트워크 입니다.

from scipy.io import mmread
import networkx as nx

data = mmread('email-enron-only.mtx')
G = nx.Graph(data, nodetype=int)
components = list(nx.connected_components(G))
print(len(components))  ## 1
core = next(nx.connected_components(G))
print(core)  ## 0 ~ 142

먼저, random failure를 통해서 robustness test를 해봅시다. 저는 25개의 step으로 plot을 그리기 위해 한 step에 5개의 노드를 랜덤하게 제거하겠습니다.

import random

number_of_steps = 25
M = G.number_of_nodes() // number_of_steps
print(M)  ## 5

이제 아래의 코드로 각 step마다 $S$ 값을 계산해주고, plot을 그려줍니다. Random failure의 경우, S 값이 linear하게 감소하며, 네트워크가 꽤 robust 함을 알 수 있습니다.

import matplotlib.pyplot as plt

num_nodes_removed = range(0, G.number_of_nodes(), M)

N = G.number_of_nodes()
C = G.copy()
random_attack_core_proportions = []
for nodes_removed in num_nodes_removed:
    # Calculation of S
    core = next(nx.connected_components(C))
    core_proportion = len(core) / N
    random_attack_core_proportions.append(core_proportion)
    
    # If there are more than M nodes, select M nodes at random and remove them
    if C.number_of_nodes() > M:
        nodes_to_remove = random.sample(list(C.nodes), M)
        C.remove_nodes_from(nodes_to_remove)
        

plt.title('Random failure')
plt.xlabel('Number of nodes removed')
plt.ylabel('Proportion of nodes in core')
plt.plot(num_nodes_removed, random_attack_core_proportions, marker='o')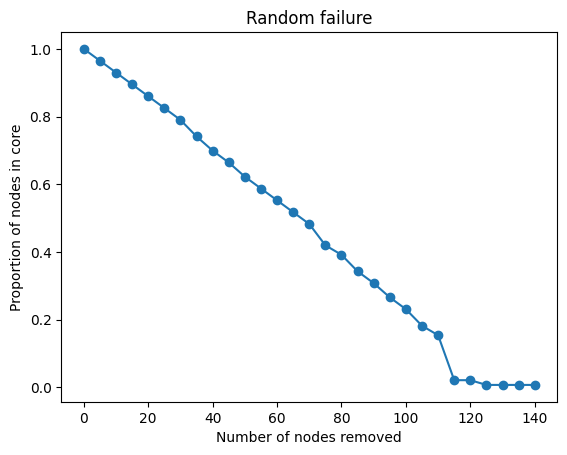

이제 아래의 코드로 attack 방식의 robustness test를 해봅시다. Random faliure와의 차이는 각 step마다 노드를 지울 때 degree가 가장 큰 5개의 노드를 선택한다는 것입니다. Plot을 보면 노드를 20개 지웠을 때 $S$ 값이 급격하게 감소하는 것을 확인할 수 있습니다. 즉, attack에 대하여 네트워크가 robust 하지 않습니다.

N = G.number_of_nodes()
number_of_steps = 25
M = N // number_of_steps

num_nodes_removed = range(0, N, M)
C = G.copy()
targeted_attack_core_proportions = []
for nodes_removed in num_nodes_removed:
    # Measure the relative size of the network core
    core = next(nx.connected_components(C))
    core_proportion = len(core) / N
    targeted_attack_core_proportions.append(core_proportion)
    
    # If there are more than M nodes, select top M nodes and remove them
    if C.number_of_nodes() > M:
        nodes_sorted_by_degree = sorted(C.nodes, key=C.degree, reverse=True)
        nodes_to_remove = nodes_sorted_by_degree[:M]
        C.remove_nodes_from(nodes_to_remove)
        
plt.title('Targeted attack')
plt.xlabel('Number of nodes removed')
plt.ylabel('Proportion of nodes in core')
plt.plot(num_nodes_removed, targeted_attack_core_proportions, marker='o')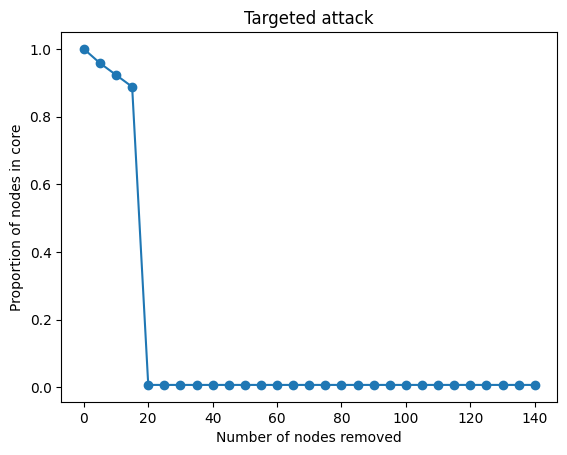

두 전략을 비교하기 위해 한 plot에 담아봤습니다. 이를 통해 네트워크의 robustness가 test 방식에 따라 극명하게 다르다는 것을 알 수 있습니다.

plt.title('Random failure vs. targeted attack')
plt.xlabel('Number of nodes removed')
plt.ylabel('Proportion of nodes in core')
plt.plot(num_nodes_removed, random_attack_core_proportions, marker='o', label='Failures')
plt.plot(num_nodes_removed, targeted_attack_core_proportions, marker='^', label='Attacks')
plt.legend()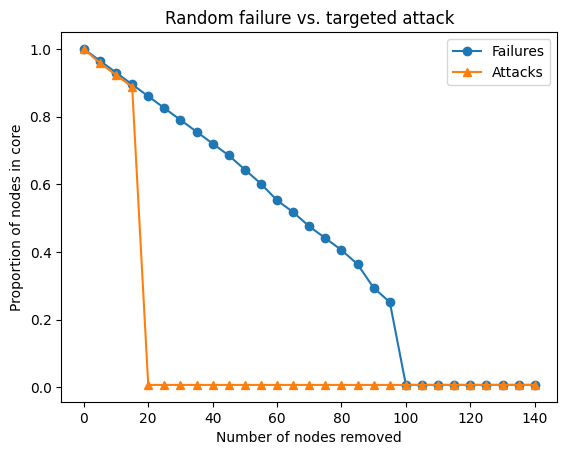

2. Core decomposition

네트워크의 core는 네트워크의 가장 조밀한 (dense) 부분으로, degree 값이 큰 노드들로 구성되어 있습니다. 이는 네트워크의 핵심 부분이기 때문에 주 분석 대상이 되며, 주로 core decomposition을 통해서 분석합니다.

Core decomposition: Degree 값이 낮은 값을 갖는 노드들부터 높은 값을 갖는 노드들을 제거해감으로써 dense한 core들을 찾아내는 절차입니다. 여기서 degree가 $k$보다 작은 노드들을 제거했을 때 얻은 core를 $k$-core 라고 합니다.

k-core decomposision의 절차는 다음과 같습니다.
(1) 먼저 $k=0$에서 시작합니다.
(2)Degree가 $k$인 노드들을 제거합니다. 이때 제거된 노드들을 $k$번째 shell이라고 하며, 남아 있는 노드들을 $(k+1)$-core라고 합니다. 
(3) $k=k+1$을 하고 (2)를 반복합니다. 만약, 남아있는 노드가 없다면 절차를 중단합니다.

 

출처: https://en.wikipedia.org/wiki/LaNet-vi

 

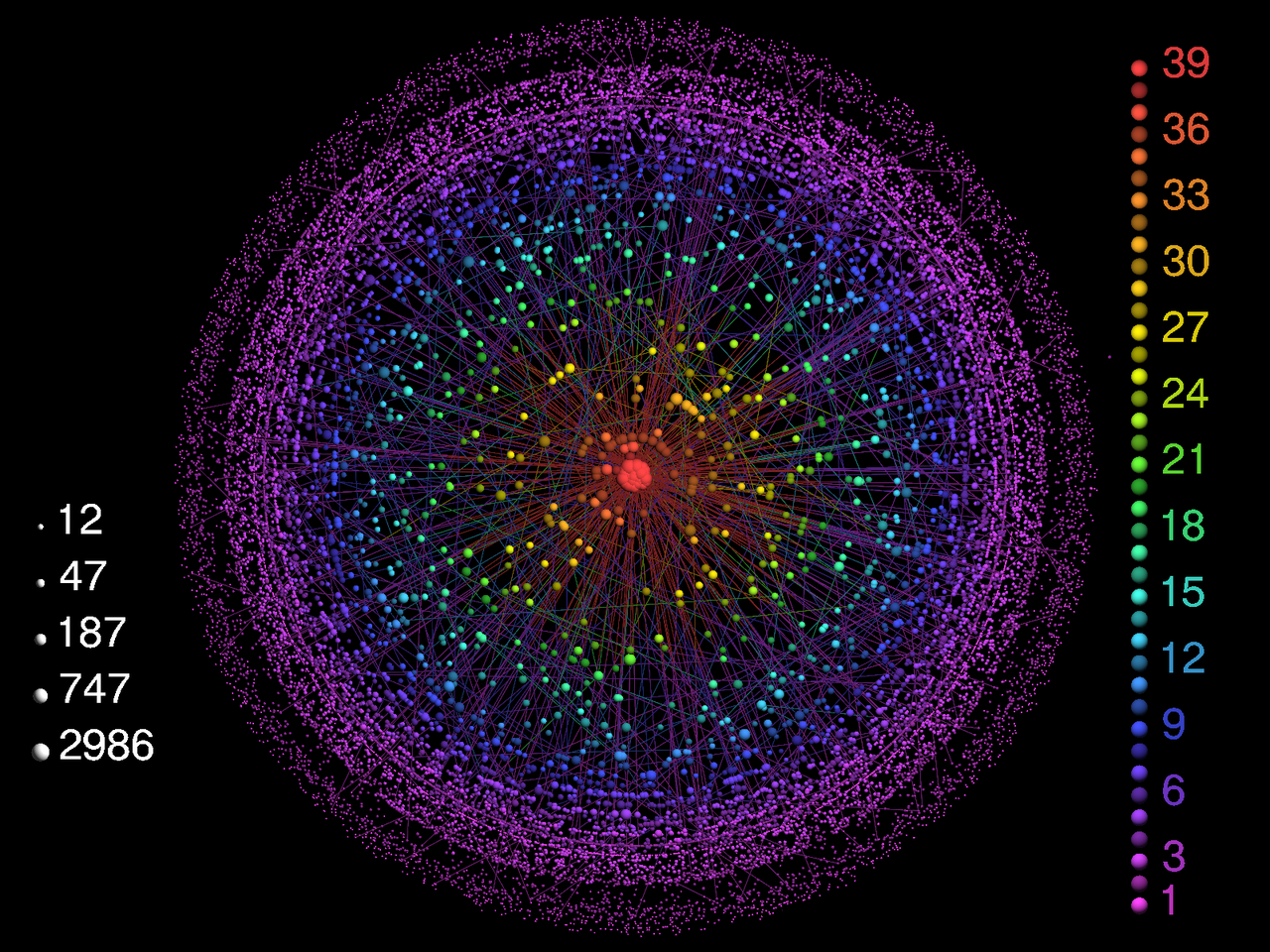
Enron 사의 이메일 데이터에 $k$-core decomposition을 적용해봅시다.
Networkx 패키지의 core_number() 매서드는 각 노드가 속하는 최대의 $k$-core를 dictionary 형태로 반환합니다.
nx.k_shell(G,k)는 $G$ 네트워크의 $k$번째 shell로 이루어지는 네트워크를 반환하며, nx.k_core(G,k)는 $k$-core로 만들어지는 네트워크를 반환합니다. 만약, 파라매터 $k$를 주지 않으면, nx.k_core 매서드는 최대 degree의 core로 이루어진 네트워크를 return 합니다.

print(nx.core_number(G)) # dict with core number of each node
nx.k_shell(G,5) # subnetwork induced by nodes in 5-shell
nx.k_core(G,6) # subnetwork induced by nodes in 6-core
nx.k_core(G) # max-degree core subnetwork

 

아래의 코드는 각 $k$-core를 시각화 하는 코드입니다. 가운데에 위치한 노드가 가장 높은 $k$-core에 속하는 노드들이고, 주변부에 위치한 노드들일수록 낮은 $k$-core에 속하는 노드들입니다. 

 

from collections import defaultdict
import matplotlib

kcores = defaultdict(list)
for n, k in nx.core_number(G).items():
    kcores[k].append(n)

kcores = dict(sorted(kcores.items(), reverse=True))

pos = nx.layout.shell_layout(G, list(kcores.values()))
cmap = plt.cm.rainbow
norm = matplotlib.colors.Normalize(vmin=0, vmax=max(nx.core_number(G).values()))

for kcore, nodes in kcores.items():
    nx.draw_networkx_nodes(G, pos, nodelist=nodes, node_color=cmap(norm(kcore)), node_size=100)
nx.draw_networkx_edges(G, pos, width=0.2)
nx.draw_networkx_labels(G, pos, font_size=9)
plt.show()

3. Assortativity

지난 포스트에서 assortativity의 정의를 다뤘습니다.

네트워크 데이터 분석 - 현실 네트워크의 특징들

네트워크 데이터 분석 - 현실 네트워크의 특징들

Assortativity란, 같은 특징을 가진 사람 또는 노드가 연결되는 현상으로, 현실의 네트워크에서 흔하게 관찰되는 현상입니다. 네트워크에 2개의 그룹이 존재하는 경우, heterophilicity (이호성)와 dyadicity (이극성) 이라는 두 가지 파라매터가 정의될 수 있습니다.

3 - 1. Heterophilicity (이호성)

Heterophilciity 란 자신과 다른 특징을 가진 대상을 좋아하는 속성이라고 보시면 됩니다. 이와 반대 되는 개념은 heterophobic 이라고 합니다. 네트워크에서 heterophilicity는 서로 다른 group에 속하는 노드들이 연결 되어있는 정도를 나타내며, 랜덤으로 생성된 그래프와 비교하며 서로 다른 group을 연결하는 edge가 더 많으면 네트워크가 heterophilic 하다고 합니다. 수학적으로는 다음과 같이 정의할 수 있습니다.

$$H = \frac{m_{01}}{\overline{m_{01}}}$$

여기서 $m_{01}$은 서로 다른 그룹의 노드들을 연결하는 edge의 개수이고, $\overline{m_{01}}=\binom{n_{0}}{1} \times \binom{n_{1}}{1} \times d = n_{0} \times n_{1} \times d$은 서로 다른 그룹의 노드들을 연결하는 edge의 평균 개수 입니다 (d: density, $d=\frac{L}{\binom{N}{2}}$). $H>1$ 이면, 네트워크가 heterophilic 하다고 하며, $H < 1$이면 네트워크가 heterophobic 하다고 합니다.

3 - 2. Dyadicity (이극성)

Dyadicity는 같은 그룹에 속하는 노드들이 연결된 정도를 나타내며, 랜덤으로 생성된 그래프와 비교할 때 같은 그룹의 노드들을 연결하는 edge가 많으면 네트워크가 dyadic 하다고 합니다. 따라서 네트워크가 heterophobic하고 dyadic 하면, assortativity가 높다고 할 수 있습니다. Dyadicity는 다음과 같이 정의 됩니다.

$$D_{i} = \frac{m_{ii}}{\overline{m_{ii}}} \text{,  } i=0 \text{ or } 1$$

여기서 $m_{ii}$는 $i$ 그룹에 속한 노드들을 연결하는 edge의 개수이며, $ \overline{m_{ii}} = \binom{n_{i}}{2} \times d = n_{0} \times (n_{0}-1) \times d$ 는 $i$ 그룹의 노드들을 연결하는 edge의 평균 개수 입니다. $D_{i} < 1$이면 네트워크가 anti-dyadic 하다고 하며, $D_{i} > 1$이면 네트워크가 dyadic 하다고 합니다.

3 - 3. 예시

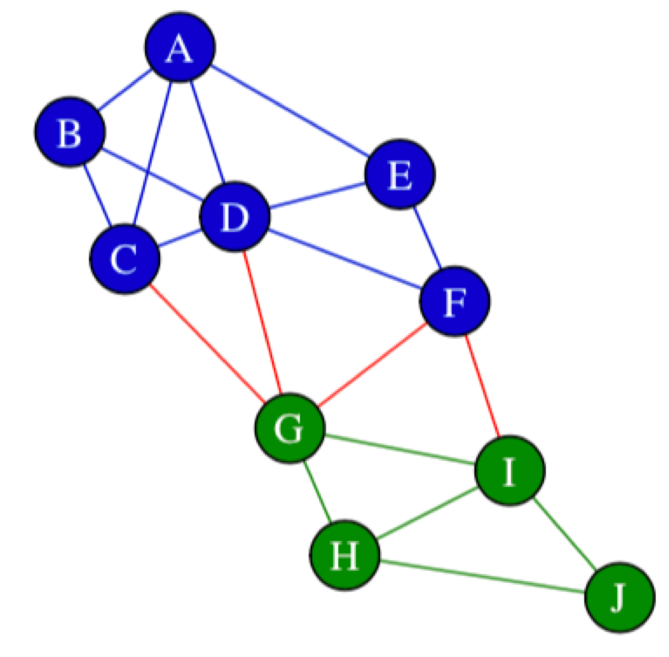
위의 네트워크를 예시로 heterophilicity와 dyadicity를 계산해봅시다.

먼저, 노의 개수는 $N=10$, edge의 개수는 $L=19$ 입니다.
또한, 파란색 노드의 수는 $n_{b} = 6$, 초록색 노드의 수는 $n_{g} = 4$ 입니다.
파란색 그룹에 속하는 노드들을 연결하는 edge의 개수는 $m_{bb} = 10$, 초록색 그룹에 속하는 노드들을 연결하는 edge의 개수는 $m_{gg} = 5$, 그리고 서로 다른 그룹에 속하는 노드들을 연결하는 edge의 개수는 $m_{bg} = 4$ 입니다.
마지막으로, 네트워크의 density는 $d=\frac{2L}{N(N-1)} = 0.42$ 입니다.

Heterophlicity를 계산해보면 다음과 같습니다.
$\overline{m_{bg}} = \binom{n_{b}}{1} \times \binom{b_{g}}{1} \times d = 6 \cdot 4 \cdot 0.42 = 10.08$ 이므로,

$$H = \frac{m_{bg}}{\overline{m_{bg}}} = \frac{4}{10.08} = 0.39 < 1$$

그러므로 이 네트워크는 heterophobic 합니다.

Dyadicity의 계산은 다음과 같습니다.
$\overline{m_{bb}} = \binom{n_{b}}{2} \ times d = \frac{6 \cdot 5}{2} \times d = 6.3$ 이므로,

$$D_{b} = \frac{m_{bb}}{\overline{m_{bb}}} = \frac{10}{6.3} = 1.59 > 1$$

따라서 이 네트워크는 dyadic 합니다.