네트워크 데이터 분석 - Community detection: Girvan-Newman algorithm

목차

 

이번 포스트에서는 네트워크에서 community를 탐지하는 알고리즘중 하나인 Girvan-Newman algorithm에 대해서 다뤄보겠습니다.

현실의 네트워크는 assortativity와 같은 이유로, 비슷한 사람 또는 노드 끼리 연결되고, 그 결과로 커뮤니티 구조가 나타난다는 것을 지난 포스트에서 다뤘습니다. 학교나 반과 같은 커뮤니티는 데이터로 주어지지만, 보통 네트워크 데이터에서 커뮤니티에 대한 정보는 주어지지 않습니다. 이러한 경우, 네트워크에서 커뮤니티들을 탐지 (community detection)할 필요가 있습니다. Community detection은 노드 클러스터링의 한 종류이며, 때로는 클러스터링보다 한 단계 더 나아가기도 합니다.

커뮤니티에 대한 더 자세한 정보는 아래의 포스트를 참고 바랍니다.

(네트워크 데이터 분석 - Communities)

네트워크 데이터 분석 - Communities

 

1. Bridge removal

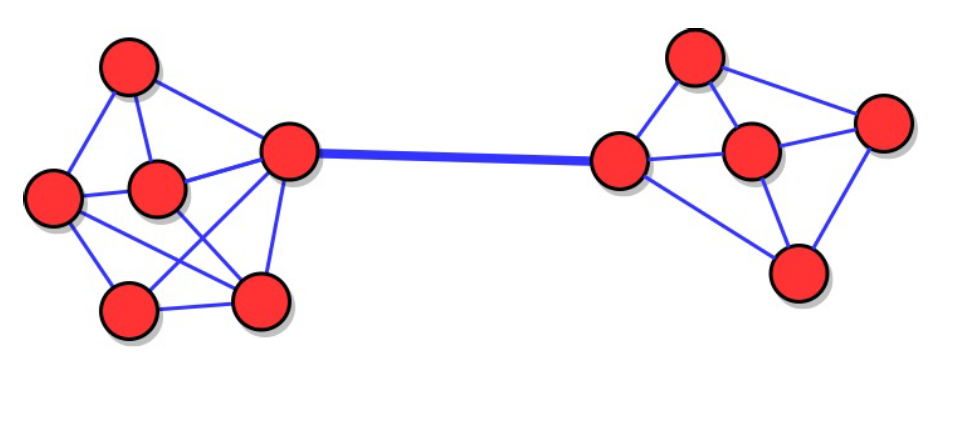
Bridge removal은 클러스터 사이를 연결하는 엣지(bridges)를 클러스터들이 고립될 때까지 제거하는 방법입니다. 이 결과로 나타난 단절된 네트워크(disconnected network)의 연결된 구성 요소들(connected components)이 우리가 찾는 커뮤니티에 해당합니다.
따라서 이 알고리즘에서 가장 중요한 요소는 bridge를 어떻게 정의하느냐입니다. 일반적으로 어떤 엣지가 적절한 측도(measure)에 대해 클러스터 내부의 엣지들(inner links)에 비해 더 크거나 작은 값을 가지면 bridge로 간주됩니다.

두 클러스터를 잇는 bridge

2. Girvan-Newman algorithm

Girvan-Newman 알고리즘은 bridge removal을 이용한 알고리즘이며, 지난 포스트에서 다뤘던 edge betweenness를 측도로 사용합니다.

(네트워크 데이터 분석 - Centrality)

네트워크 데이터 분석 - Centrality

Edge betweenness는 정보가 지나가는 가장 짧은 경로들(shortest path)이 해당 엣지를 얼마나 자주 지나가는지를 나타내는 측도(measure)입니다. 따라서, bridge는 높은 betweenness 값을 가져야 합니다. 이는 정보가 한 커뮤니티에서 다른 커뮤니티로 전달되려면 반드시 bridge를 통해야 하기 때문입니다. 반대로, 클러스터 내부 edge의 경우, 이 edge를 지나지 않고도 정보를 전달할 수 있는 다른 경로가 많기 때문에 edge betweenness가 상대적으로 낮습니다. 

2 - 1. Procedure

Girvan-Newman 알고리즘의 절차는 다음과 같습니다.

1. 모든 edge의 betweenness를 계산합니다.
2. 가장 큰 betweenness 값을 가진 edge를 제거합니다. 만약 같은 값을 가지는 edge가 여러 개 있다면, 랜덤하게 하나를 선택해서 제거합니다.
3. 남은 edge들의 betweenness를 다시 계산합니다.
4. 2~3을 모든 edge가 제거될 때까지 반복합니다.

Girvan-Newman 알고리즘은 divisive hierarchical clustering 입니다. 왜냐하면, 각 iteration마다 네트워크를 계속 분할해서 최종적으로 모든 노드가 singleton이 되기 때문이죠. 이 결과는 dendrogram으로 나타낼 수 있습니다.
네트워크의 hierarchical clustering에 대해 더 알고 싶으시면 아래의 포스트를 참고해주세요.

네트워크 데이터 분석 - partitioning & clustering

 

2 - 2. 한계

• 각 iteration마다 모든 edge의 betweenness를 다시 계산해야 하므로, 알고리즘이 꽤 느립니다.
• Girvan-Newman algorithm의 결과는 $N$개의 partition들입니다. 이중 어떤 parition을 선택해야 할지에 대해서는 기준이 없습니다.

3. 코딩 예시

이번에도 networkx에서 제공해주는 Zachary's karate club 데이터를 이용해 봅시다.

import networkx as nx

K = nx.karate_club_graph()
club_color = {
    'Mr. Hi': 'orange',
    'Officer': 'lightblue',
}
pos = nx.spring_layout(K, seed=7)
node_colors = [club_color[K.nodes[n]['club']] for n in K.nodes]
nx.draw(K, pos, node_color=node_colors, with_labels=True)

Zachary's karate club 네트워크

Networkx에는 nx.community.girvan_newman() 라는 매서드가 Girvan-Newman algorithm을 시행해줍니다. 이 매서드는 알고리즘으로 생성되는 모든 partition들의 iterator를 반환합니다. list()를 이용하여 출력하면, 모든 partition들을 볼 수 있습니다.

partitions = nx.community.girvan_newman(K)
print(list(partitions)) ## list of partitions

아쉽게도 networkx는 이 partition들을 이용해서 dendrogram을 그려주지는 않습니다. 결국 주어진 partition을 이용하여 직접 dendrogram을 그려야 하는데, 이 과정이 좀 복잡합니다. 나눠서 하나씩 알아보죠.

Scipy의 dendrogam 함수를 사용할 것이기 때문에 linkage matrix를 구성하는 것이 핵심입니다.
아래의 코드는 먼저 Girvan-Newman 알고리즘으로 생성된 모든 클러스터의 dictionary (init_node2comminity_dict) 를 만듭니다. Girvan-Newman의 결과에는 클러스터가 하나인 partition(즉, 네트워크 전체를 하나의 커뮤니티로 보는 partition)은 존재하지 않기 때문에 직접 dictionary에 넣어줘야 합니다. 첫 번째 partition이 네트워크를 둘로 분할하는 partition이기 때문에 여기에 union()을 이용하여 전체 노드를 하나의 클러스터로 만들어줍니다.

from itertools import chain, combinations
import matplotlib.pyplot as plt
from scipy.cluster.hierarchy import dendrogram, cut_tree

partitions = list(partitions)

# record all clusters generated as dictionary
node_id = 0
init_node2community_dict = {node_id: partitions[0][0].union(partitions[0][1])}
for comm in partitions:
    for subset in list(comm):
        if subset not in init_node2community_dict.values():
            node_id += 1
            init_node2community_dict[node_id] = subset

Dendrogram은 tree 입니다. 따라서 dendrogram을 그리기 위해서는 각 클러스터 별로 자식 노드 (또는 클러스터)를 정해줘야 합니다. Girvan-Newman 알고리즘에서 한 partition에 있는 클러스터중 하나는 반드시 바로 다음 partition의 클러스터 2개가 합쳐진 형태입니다. 따라서, 두 클러스터의 교집합이 공집합이고, 합집합이 해당 클러스터와 일치한다면, 이 두 클러스터가 자식 노드 (또는 클러스터)가 됩니다. 아래의 코드는 각 클러스터의 id를 key로, 그리고 자식 클러스터를 value로 갖는 dictionary를 생성합니다.

# turning this dictionary to the desired format
node_id_to_children = {e: [] for e in init_node2community_dict.keys()}
for node_id1, node_id2 in combinations(init_node2community_dict.keys(), 2):
    for node_id_parent, group in init_node2community_dict.items():
        if len(init_node2community_dict[node_id1].intersection(init_node2community_dict[node_id2])) == 0 and group == init_node2community_dict[node_id1].union(init_node2community_dict[node_id2]):
            node_id_to_children[node_id_parent].append(node_id1)
            node_id_to_children[node_id_parent].append(node_id2)

 

크기가 1인 클러스터는 결국 노드가 하나뿐인 클러스터로, 이런 클러스터에는 노드의 이름을 붙여줍니다.

node_labels = dict()
for node_id, group in init_node2community_dict.items():
    if len(group) == 1:
        node_labels[node_id] = list(group)[0]
    else:
        node_labels[node_id] = ''

 

아래의 코드는 Girvan-Newman 알고리즘의 마지막 partition에서부터 시작해서 각 클러스터에 rank를 부여합니다. 마지막 줄은 모든 노드를 가지는 클러스터에 최상위 rank를 부여합니다.

subset_rank_dict = dict()
rank = 0
for e in partitions[::-1]:
    for p in list(e):
        if tuple(p) not in subset_rank_dict:
            subset_rank_dict[tuple(sorted(p))] = rank
            rank += 1
subset_rank_dict[tuple(sorted(chain.from_iterable(partitions[-1])))] = rank

 

아래의 함수는 두 클러스터의 거리(또는 dendrogram의 높이)를 계산해줍니다. 각 클러스터의 거리가 유일한 값이 되도록 rank를 사용하였습니다.

def get_merge_height(sub):
    sub_tuple = tuple(sorted([node_labels[i] for i in sub]))
    n = len(sub_tuple)
    other_same_len_merges = {k: v for k, v in subset_rank_dict.items() if len(k) == n}
    min_rank, max_rank = min(other_same_len_merges.values()), max(other_same_len_merges.values())
    range = (max_rank-min_rank) if max_rank > min_rank else 1
    return float(len(sub)) + 0.8 * (subset_rank_dict[sub_tuple] - min_rank) / range

 

이제 node_id_to_childrend을 사용하여 directed tree를 생성해주고 out_degree 값을 통해 leaves와 inner_nodes를 구분해줍니다. 그리고 subtree는 각 클러스터에 대해 그 클러스터에 속하는 노드들의 리스트를 값으로 가집니다. 그리고 이 subtree를 key로 사용하여, inner_nodes를 정렬해줍니다. 이렇게 하면, 가장 마지막에 있는 inner_node는 모든 노드를 가지는 partition, 즉 dendrogram의 root가 됩니다.

# finally drawing dendrogram
G = nx.DiGraph(node_id_to_children)
nodes = G.nodes()
leaves = set(n for n in nodes if G.out_degree(n) == 0 )
inner_nodes = [n for n in nodes if G.out_degree(n) > 0 ]

# Compute the size of each subtree
subtree = dict( (n, [n]) for n in leaves )
for u in inner_nodes:
    children = set()
    node_list = list(node_id_to_children[u])
    while len(node_list) > 0:
        v = node_list.pop(0)
        children.add( v )
        node_list += node_id_to_children[v]
    subtree[u] = sorted(children & leaves)

inner_nodes.sort(key=lambda n: len(subtree[n])) # <-- order inner nodes ascending by subtree size, root is last

이제 정렬된 inner_nodes에 for 구문을 이용하여 linkage matrix를 만들어줍니다.
Linkage matrix의 첫번째와 두번째 열은 클러스터를 나타내며, 세번째 열은 두 클러스터 사이의 거리, 그리고 마지막 열은 새롭게 생성된 클러스터의 원소의 개수를 의미합니다. 각 행은 두 자식 클러스터가 합쳐져서 부모 클러스터가 되는 것을 나타내는 것이라고 보면 됩니다. 

# Construct the linkage matrix
leaves = sorted(leaves)
index  = dict( (tuple([n]), i) for i, n in enumerate(leaves) )
Z = []
k = len(leaves)
for i, n in enumerate(inner_nodes):
    children = node_id_to_children[n]
    x = children[0]
    y = children[1]
    z = tuple(sorted(subtree[x] + subtree[y]))
    i, j = index[tuple(sorted(subtree[x]))], index[tuple(sorted(subtree[y]))]
    Z.append([i, j, get_merge_height(subtree[n]), len(z)]) # <-- float is required by the dendrogram function
    index[z] = k
    k += 1

# dendrogram
plt.figure()
dendrogram(Z, labels=[node_labels[node_id] for node_id in leaves])

Girvan-Newman 알고리즘의 결과를 나타낸 dendrogram

아래의 코드를 이용해서 실제 네트워크와 Girvan-Newman 알고리즘의 결과를 비교해보겠습니다. Dendrogram으로부터 2개의 클러스터를 얻기 위해 cut_tree() 매서드를 사용했습니다. 여기서 주의할 점은 cut_tree()의 결과로 나온 group label의 sequence는 실제 노드의 순서 (0,1,2,3...) 이 아니라 dendrogram을 만들 때 사용한 leaves의 순서라는 점입니다. 그래서 정확한 순서의 cluster label을 얻으려면, 아래처럼 따로 mapping을 해줘야 합니다.

결과를 비교해보면, 실제와 다른 노드는 2번과 8번 노드뿐 입니다. 상당히 실제에 가깝게 community를 찾아낸 것을 알 수 있습니다.

two_cluster_label = cut_tree(Z, n_clusters=2).flatten()
node_seq = [node_labels[node_id] for node_id in leaves]
mapping = {v:two_cluster_label[i] for i,v in enumerate(node_seq)}
two_cluster_label = [mapping[i] for i in range(len(node_seq))]
    
fig = plt.figure(figsize=(15, 6))
pos = nx.spring_layout(K, seed=7)
plt.subplot(1, 2, 1)
node_colors = ['lightblue' if label == 0 else 'orange' for label in two_cluster_label]
nx.draw(K, with_labels=True, node_color=node_colors, pos=pos)
plt.title('Predicted communities')

plt.subplot(1, 2, 2)
node_colors = [club_color[K.nodes[n]['club']] for n in K.nodes]
nx.draw(K, with_labels=True, node_color=node_colors, pos=pos)
plt.title('Actual communities')

 

실제와 Girvan-Newman의 결과 비교