Random Walks on Groups - 서론

목차

 

 

제가 최근에 공부한 군 위에서의 랜덤워크 (random walks on groups)의 개요에 대해서 몇몇 포스트를 써보고자 합니다.

1. What is it?

가장 기본적인 랜덤워크를 생각해봅시다.
실선 위 원점에서 시작하고, 동전의 앞면이 나오면 +1, 뒷면이 나오면 -1 만큼 움직인다고 합시다. 그리고 n 번쨰 동전에 대한 확률변수를 $X_{n}$ 이라고 정의합시다. 그렇다면 독립적으로 n 번째 동전을 던졌을 때의 위치는 $S_{n} = X_{1} + X_{2} + \dots + X_{n}$ 이 됩니다. 그러면 대수의 법칙 (Law of large number)에 의하여 almost surely $\frac{S_{n}}{n}$은 0으로 수렴하고, 중심극한 정리 (Central limit theorem)에 의해 $\sqrt{n} \left( \frac{S_{n}}{n} \right)$은 표준정규분포로 converge in distribution 한다는 것을 아마 확률론이나 통계학을 공부하면 배우셨을 것입니다.
확률론의 관점에서 봤을 때, 기본적인 랜덤워크는 독립적인 real-valued random variable들을 합을 하는 방식입니다.
여기에서 한걸음 더 나아가 Random walks on groups는 실수를 일반적인 군 (group)으로 일반화합니다.

2. 예시 - Grid 위에서의 random walk

$G=\mathbb{Z}^{d}$, $X=\{\text{d-dimensional square grid}\}$ 라고 생각해봅시다.
(여기서 $X$는 임의의 geometric space라고 보면 됩니다.)
그러면 G의 원소는 $g =(t_{1}, t_{2}, \dots, t_{d})$ 이고, random walk의 시작점 $o \in X$은 $o = (x_{1}, x_{2}, \dots, x_{d})$이 됩니다.
그리고 다음을 정의합니다.
Def) A group action of $G$ on a metric space $\left( X, d \right)$ is a homomorphism $\rho: G \to Isom(X)$ where $Isom(X)=\{f: X \to X \text{ is bijective such that }d(f(x), f(y)) = d(x,y) \text{ for all }x,y\}$

그리고 원점에 대해서 다음과 같은 notation을 사용합니다.
$$o \in X, go=\rho(g)(o)$$
그러면 $go = (x_{1}+t_{1}, \dots, x_{d}+t_{d} ) $으로 시작점에 대한 group action을 표현할 수 있습니다.

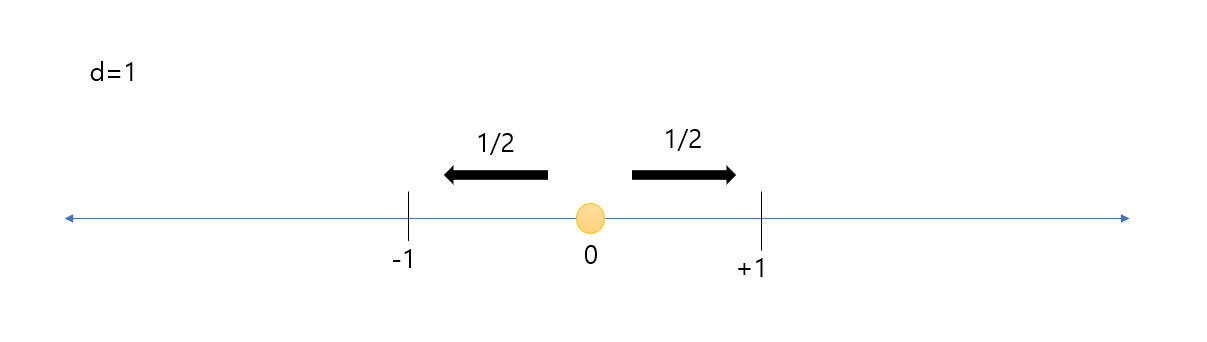
이제 $d=1$인 경우를 생각해봅니다. 그러면 $X$는 $\mathbb{Z}$와 isomorphic 합니다.
그러면 $G=\mathbb{Z}$ 위에서의 확률 측도 (probability measure) $\mu = \frac{1}{2}\left( \delta_{+1} + \delta_{-1} \right)$ 를 정의할 수 있습니다. ($\delta$는 Dirac measure 입니다.)

3. Setup

앞으로 쭉 사용할 setup을 정의하면 다음과 같습니다.

Define $W_{n}:=g_{1} g_{2} \dots g_{n} $.
($W_{n}$) is called a sample path of the random walk

섹션 1에서 본 가장 간단한 random walk와 비교하면 $S_{n}$은 $W_{n}$의 special case 임을 알 수 있습니다.
($S_{n} = X_{1} + X_{2} + \dots + X_{n} \longrightarrow W_{n}=g_{1} g_{2} \dots g_{n}$)

(여기서 주의할 점은 ($W_{n}$) 이 iid가 아니라는 점입니다!)

앞으로 group action $ G \to Isom(X)$ 이 존재한다면, 우리는 원점 $o \in X$를 고정하고, $(W_{n} \cdot o) \in X$에 대해 살펴볼 것입니다.

4. Why?

그렇다면 왜 굳이 일반적인 group 위에서의 random walk를 연구하는 것일까요?

이해를 위해서 두 가지의 예시를 들어봅시다.

1. 2차원 grid 위에서의 random walk

첫번째는 2차원 grid 위에서의 random walk 입니다.

원점: $o=(0,0)$
확률 측도: $\mu=\frac{1}{4}(\delta_{(0,+1)} + \delta_{(0,-1)} + \delta_{(+1,0)} + \delta_{(-1,0)} )$

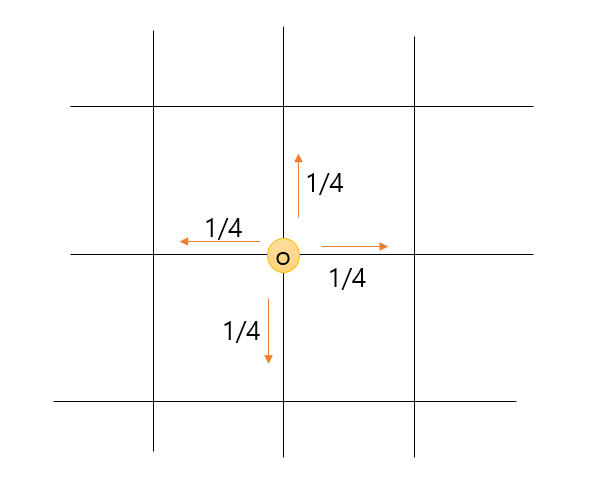
앞으로의 포스트에서 제대로 정의하겠지만, 2차원 grid 위에서의 random walk은 다음과 같은 특성을 가집니다.
1. random walk이 recurrent 하다. (n이 무한히 커지면, random walk이 원점을 무한히 자주 재방문할 확률이 1이다.)
2. random walk의 speed가 0이다. (n이 무한히 커지면, 원점으로부터의 거리가 평균적으로 0이다.)

2. 4-valent tree

두번째는 4-valent tree 입니다.

군 (group): $Isom(X)$
원점: $o=(0,0)$
확률 측도: $\mu=\frac{1}{4}(\delta_{a} + \delta_{a^{-1}} + \delta_{b} + \delta_{b^{-1}} )$

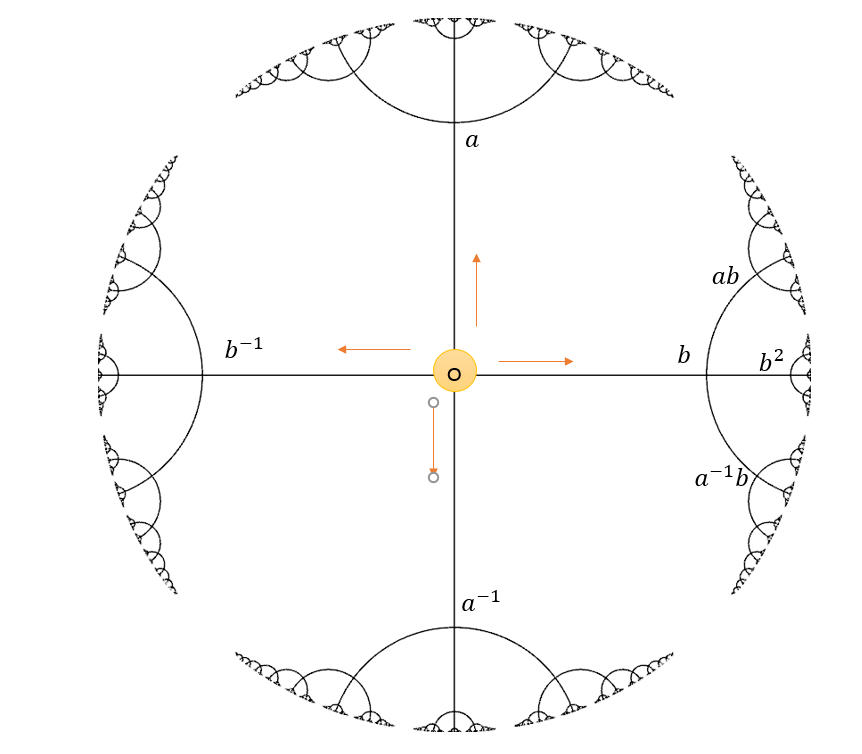
2차원 grid의 경우와 다르게 4-valent tree는 다음과 같은 특성을 가집니다.
1. random walk이 trainsient 하다. (recurrent하지 않다.)
2. random walk의 speed가 0 보다 크다. (n이 무한히 커지면, 원점으로부터의 거리가 평균적으로 0보다 크다.)

기하학적으로 2차원 grid는 flat 하고, 따라서 곡률 (culvature)가 0 입니다. 한편, 4-valent tree는 hyperbolic 하며, 곡률이 0보다 작다는 것이 알려져있습니다.
두 공간은 2차원에서 정의되지만, 기하학적으로 다른 특성을 가지고 있으며, random walk 또한 다른 특성을 가지고 있다는 것을 알 수 있습니다. 즉, random walk을 통해서 공간의 특성을 identify 하고, 서로 다른 두 공간의 다른 특성을 찾아낼 수 있기 때문에 일반적인 군 (group) 위에서의 random walk이 중요한 의미를 가지는 것입니다.