목차
이번 포스트에서는 커뮤니티 탐지 알고리즘중 modularity(모듈성)를 이용하는 알고리즘들에 대해서 다루겠습니다.
1. Modularity(모듈성)
지난 포스트에서는 Girvan-Newman 알고리즘을 이용하여 네트워크의 partition을 구했습니다. 하지만 Girvan-Newman 알고리즘은 hierarchical clustering을 이용하기 때문에 여러 partition들을 제시할 뿐, 어떤 partition을 선택해야하는 지에 대해서는 아무런 답을 주지 않습니다. (Girvan-Newman 알고리즘에 더 알고 싶으시면 아래의 링크를 참고해 주세요.)
네트워크 데이터 분석 - Community detection: Girvan-Newman algorithm
목차 " data-ke-type="html">HTML 삽입미리보기할 수 없는 소스 이번 포스트에서는 네트워크에서 community를 탐지하는 알고리즘중 하나인 Girvan-Newman algorithm에 대해서 다뤄보겠습니다.현실의 네트워크는
sanghn.tistory.com
결국 커뮤니티 구조를 나타내는 가장 좋은 partition을 선택하려면 어떤 기준이 존재 하거나 partition의 퀄리티를 측정하는 측도가 있어야 할 것입니다. 이를 quality function 이라고 합니다.
1 - 1. 정의
Modularity는 quality function의 한 종류입니다. Modualrity의 원칙은 주어진 네트워크와 랜덤 네트워크를 비교해서 각 커뮤니티를 평가하는 것입니다. 이때, 랜덤 네트워크는 원래 네트워크의 degree sqeuqnce를 유지해야 합니다.
Modularity는 각 커뮤니티에 대해서 해당 커뮤니티의 내부 edge의 수와 랜덤하게 네트워크를 생성할 경우 내부 edge 개수의 기댓값의 차이를 계산합니다. 만약 네트워크가 랜덤하게 생성 되었다면, 어떤 partition이든 클러스터의 modularity 값은 낮게 나올 것입니다. 왜냐하면 클러스터의 내부 edge의 수가 기댓값과 비슷할 것이기 때문입니다. 반대로, 만약 클러스터의 내부 edge 수가 기댓값보다 많이 크다면, 이는 랜덤한 과정에서 생성되었을 가능성이 낮음을 시사하고, modularity는 높은 값을 가질 것입니다.
Modularity의 수학적 정의는 다음과 같습니다.
$$Q = \frac{1}{L}\sum_{C}\left(L_{C} - \frac{k^{2}_{C}}{4L} \right)$$
- $L$ = 네트워크의 edge 개수,
- $L_{C}$ = 커뮤니티 $C$의 내부 edge 개수
- $k_{C}$ = 커뮤니티 $C$의 degree
- $\frac{k^{2}_{C}}{4L}$ = 커뮤니티 $C$의 내부 edge 수의 기댓값
그렇다면 커뮤니티 $C$의 내부 edge 수의 기댓값이 $\frac{k^{2}_{C}}{4L}$인 이유는 무엇일까요?
랜덤한 edge는 랜덤하게 선택된 stub의 쌍을 연결면서 형성됩니다. 여기서 stub이란 edge를 반으로 쪼갠 것이라고 생각하시면 됩니다. (아래의 그림을 참고 바랍니다.) 그러면 커뮤니티 $C$에 부착된 stub의 수는 곧 $k_{C}$가 됩니다.
이제 확률을 생각 해보겠습니다. 먼저, $k_{C}$에 부착된 stub를 선택할 확률은 $\frac{k_{C}}{2L}$ 입니다. 왜냐하면 네트워크 전체의 edge 개수는 $L$이고, 하나의 edge는 2개의 stub을 만들어내기 때문입니다.
이제 한 edge가 커뮤니티 $C$의 내부 edge가 될 확률을 생각 해보겠습니다. 커뮤니티 $C$에 속하는 두 노드를 연결하려면, 커뮤니티 $C$에 부착된 stub 2개가 선택되어야 합니다. 그러면 $C$에서 2개의 stub이 선택될 확률은 대략 $p_{C} = \frac{k_{C}}{2L} \cdot \frac{k_{C}}{2L} = \frac{k^{2}_{C}}{4L^{2}}$이 됩니다.
결국, 네트워크에 $L$개의 edge가 있고, 각 edge는 $p_{C}$의 확률로 커뮤니티 $C$에 속하기 때문에, 커뮤니티 $C$의 내부 edge 개수의 기댓값은 $\frac{k^{2}_{C}}{4L^{2}} \times L = \frac{k^{2}_{C}}{4L}$이 됩니다.


1 - 2. Modularity의 특징
- 모든 네트워크의 각 클러스터는 $Q<1$을 만족합니다.
- 모든 노드가 하나의 커뮤니티에 속한 경우 $Q=0$ 입니다.
- $Q$는 음수가 될 수도 있습니다. 예를 들어, 각 노드가 하나의 커뮤니티인 경우가 있습니다.
- 대부분의 네트워크에서 $Q$는 0과 1 사이의 non-trivial한 최댓값을 같습니다.
1 - 3. 다른 네트워크로의 확장
Modularity는 다른 네트워크로도 확장이 가능합니다.
(1) Directed network의 경우,
$$Q_{d} = \frac{1}{L} \sum_{C}\left(L_{C} - \frac{k^{in}_{C}k^{out}_{C}}{L} \right) $$
- $L$ = 네트워크의 edge 개수,
- $L_{C}$ = 커뮤니티 $C$의 내부 edge 개수
- $k^{in}_{C}$ = 커뮤니티 $C$에 속한 노드의 in-degree 합
- $k^{out}_{C}$ = 커뮤니티 $C$에 속한 노드의 out-degree 합
(2) Weighted network의 경우,
$$Q_{w} = \frac{1}{W} \sum_{C}\left(W_{C} - \frac{s^{2}_{C}}{4W} \right) $$
- $W$ = 네트워크 edge의 weight 합
- $W_{C}$ = 커뮤니티 $C$의 내부 edge의 weight 합
- $s_{C}$ = 커뮤니티 $C$에 속한 노드들의 strength의 합
(3) Directed and weighted network의 경우,
$$Q_{dw} = \frac{1}{W} \sum_{C}\left(W_{C} - \frac{s^{in}_{C}s^{out}_{C}}{W} \right) $$
- $W$ = 네트워크 edge의 weight 합
- $W_{C}$ = 커뮤니티 $C$의 내부 edge의 weight 합
- $s^{in}_{C}$ = 커뮤니티 $C$에 속한 노드들의 in-strength의 합
- $s^{out}_{C}$ = 커뮤니티 $C$에 속한 노드들의 out-strength의 합
Modularity는 Girvan-Newman 알고리즘의 결과로 얻은 partition중 최선의 partition을 찾기 위해 도입 되었습니다.
하지만 바로 modularity $Q$를 최대화하면 어떻게 될까요? Modularity의 최댓값을 구하려면 네트워크의 모든 partition을 고려해야 하는데, 그 경우의 수가 굉장히 많기 때문에 직접 최적화(optimization)를 하는 것은 매우 어려운 문제입니다. 따라서 modularity를 이용하되, 합리적인 후보의 partition들만 추려내어 검토하는 알고리즘을 만드는 것이 중요합니다.
1 - 4. 코딩 예시
이번 포스트에서도 networkx에서 제공하는 Zachary의 가라테 클럽 데이터를 사용하겠습니다.
import networkx as nx
import random
import matplotlib.pyplot as plt
K = nx.karate_club_graph()
club_color = {
'Mr. Hi': 'orange',
'Officer': 'lightblue',
}
pos = nx.spring_layout(K, seed=7)
node_colors = [club_color[K.nodes[n]['club']] for n in K.nodes]
nx.draw(K, pos, node_color=node_colors, with_labels=True)
먼저 다음과 같이 실제 파티션(empirical partition)의 modularity를 계산해보겠습니다. Networkx에서는 nx.community.quality.modularity() 매서드를 이용할 수 있습니다. 실제 파티션의 modularity 값은 0.391 정도가 나오는 것을 확인 할 수 있습니다.
groups = {
'Mr. Hi': set(),
'Officer': set(),
}
for n in K.nodes:
club = K.nodes[n]['club']
groups[club].add(n)
empirical_partition = list(groups.values())
print(nx.community.quality.modularity(K, empirical_partition))
# 0.39143756676224206이제 비교를 위해 다음과 같이 그룹을 랜덤으로 배정해보겠습니다.
random.seed(1993)
random_nodes = random.sample(K.nodes, 17)
random_partition = [set(random_nodes),
set(K.nodes) - set(random_nodes)]
random_node_colors = ['orange' if n in random_nodes else 'lightblue' for n in K.nodes]
nx.draw(K, pos, node_color=random_node_colors)
그리고 이 랜덤한 네트워크에 대해 modularity를 계산해보면 -0.030 정도로, modularity의 이론에 따라 실제 파티션보다 값이 낮게 나오는 것을 확인할 수 있습니다.
print(nx.community.quality.modularity(K, random_partition))
# -0.0301437379359457142. Newman's greedy algorithm
2 - 1. Procedure
Newman's greedy algorithm의 절차는 다음과 같습니다.
- 각 노드를 하나의 community로 놓고 시작합니다.
- $Q$를 가장 많이 증가시키는 (또는 가장 적게 감소시키는) community 둘을 합칩니다.
- 모든 노드가 하나의 커뮤니티에 속할 때까지 2를 반복합니다.
- 만들어진 partition중 가장 modularity가 큰 partition을 선택합니다.
2 - 2. 코딩 예시
Networkx에는 nx.community.greedy_modularity_communities() 매서드가 Newman's greedy 알고리즘을 시행합니다.
partition = nx.community.greedy_modularity_communities(K)
print(partition)아래의 코드를 이용해서 Newman's greedy 알고리즘의 결과와 실제 네트워크를 비교해 볼 수 있습니다.
흥미롭게도 알고리즘은 3개의 커뮤니티를 탐지합니다.
newman_node_groups = [0] * K.number_of_nodes()
group_code = 0
for group in nx.community.greedy_modularity_communities(K):
for node in group:
newman_node_groups[node] = group_code
group_code += 1
fig = plt.figure(figsize=(15, 6))
pos = nx.spring_layout(K, seed=7)
plt.subplot(1, 2, 1)
color_map = {0: 'lightblue', 1: 'green', 2: 'orange'}
newman_node_color = [color_map[i] for i in newman_node_groups]
nx.draw(K, pos, node_color=newman_node_color, with_labels=True)
plt.title('Predicted communities')
plt.subplot(1, 2, 2)
node_colors = [club_color[K.nodes[n]['club']] for n in K.nodes]
nx.draw(K, with_labels=True, node_color=node_colors, pos=pos)
plt.title('Actual communities')
2 - 3. 한계
- 각 step마다 modularity를 최대화하기 때문에 알고리즘이 greedy합니다. 따라서, suboptimal한 modularity에 갇힐 가능성이 높습니다.
- Unbalanced한 partition을 도출하는 경향이 있습니다. 어떤 커뮤니티에는 많은 노드들이 속하게 되고, 다른 커뮤니티에는 적은 수의 노드가 속하게 됩니다.
3. Louvain algorithm
3 - 1. Procedure
- 각 노드를 하나의 community로 놓고 시작합니다.
- 노드를 다음과 같이 순회합니다: 각 노드는 현재 partition에 대해 modularity 증가($\Delta Q$)가 가장 큰 이웃의 커뮤니티에 배정됩니다. 더 이상 $Q$를 증가시킬 수 없을 때까지 모든 노드는 반복적으로 검토됩니다.
- 2번 과정에서 얻은 각 커뮤니티를 supernode로 갖는 weighted supernetwork로 네트워크를 변형합니다. 서로 다른 supernode를 연결하는 edge의 weight는 다른 커뮤니티와 연결된 edge의 수가 됩니다. 그리고 각 supernode는 자기 자신을 연결하는 edge(또는 loop)를 가지며, 그 weight은 해당 커뮤니티 내부의 edge의 수$\times 2$(해당 커뮤니티 내부 degree의 합)가 됩니다.
- 더 이상 modularity $Q$가 증가하지 않을 때까지 2~3번 과정을 반복합니다.
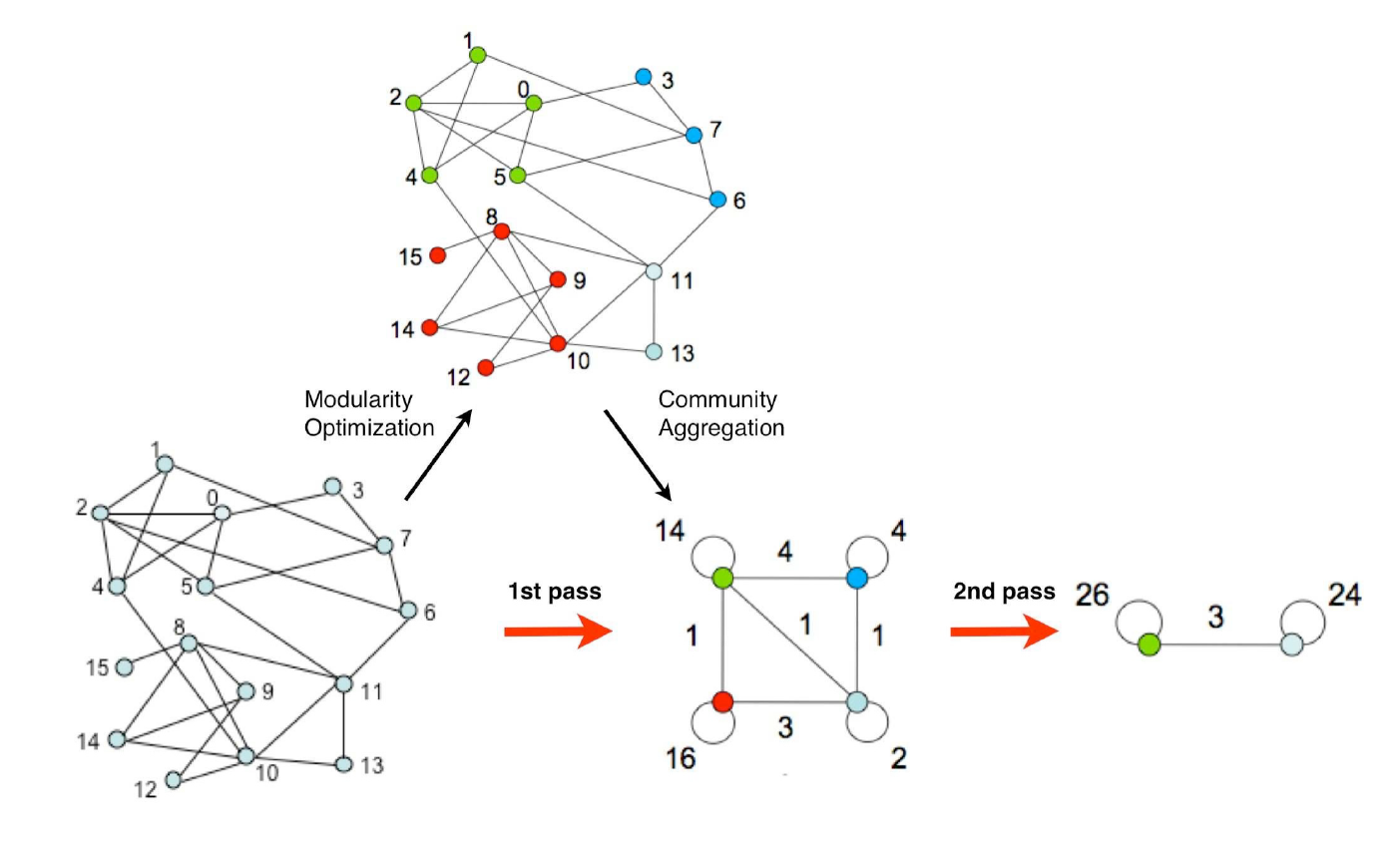
3 - 2. 코딩 예시
Networkx 패키지에는 Louvain 알고리즘이 없기 때문에 python-Louvain 패키지를 따로 설치해야 합니다.
이 패키지의 community_louvain.best_partition() 매서드는 Louvain 알고리즘을 시행하여 최적의 partition을 반환합니다.
#!pip install python-louvain
from community import community_louvain
partition_dict = community_louvain.best_partition(K)
print(partition_dict)아래의 코드로 알고리즘의 결과와 실제 네트워크를 비교해 보면, Louvain 알고리즘도 Newman의 경우와 같이, 3개의 커뮤니티를 탐지한다는 것을 알 수 있습니다.
fig = plt.figure(figsize=(15, 6))
pos = nx.spring_layout(K, seed=7)
plt.subplot(1, 2, 1)
color_map = {0: 'orange', 1: 'lightblue', 2: 'green'}
louvain_node_color = [color_map[v] for k,v in partition_dict.items()]
nx.draw(K, pos, node_color=louvain_node_color, with_labels=True)
plt.title('Predicted communities')
plt.subplot(1, 2, 2)
node_colors = [club_color[K.nodes[n]['club']] for n in K.nodes]
nx.draw(K, with_labels=True, node_color=node_colors, pos=pos)
plt.title('Actual communities')
3 - 3. 한계와 강점
- Newman의 알고리즘과 같이, Louvain 알고리즘도 greedy 합니다. 따라서, suboptimal한 modularity에 갇힐 수 있습니다.
- 노드가 방문 되는 순서에 따라 결과가 달라질 수 있습니다.
- 한번의 iteration 이후, 네트워크를 supernetwork로 압축시키기 때문에 알고리즘이 굉장히 빠릅니다. 따라서 굉장히 큰 네트워크를 다룰 때에 유리합니다.
4. Modularity 최적화의 한계
- Modularity의 최댓값은 네트워크가 클수록 더 크게 나타나는 경향이 있습니다. 따라서 modularity를 통해 네트워크 간의 partition을 비교하는 데에 사용할 수 없습니다.
- 랜덤 네트워크는 커뮤니티 구조가 없음에도, 꽤 큰 modularity를 가지는 경우가 있습니다.
- 최대의 modularity가 반드시 최선의 partition에 대응되는 것은 아닙니다. 특정 크기보다 작은 커뮤니티는 탐지되지 않을 수도 있습니다. 이를 해상 한계(resolution limit)이라고 합니다. 아래의 그림이 예시가 되는 네트워크입니다. 이 네트워크에서 최적의 커뮤니티 구조는 각 clique(완전히 연결된 사각형)를 커뮤니티로 갖는 것입니다. 그러나 modularity는 2개의 사각형이 하나의 커뮤니티로 묶일 때 최댓값을 갖습니다.

 Skypainter
Skypainter