목차
지난 포스트에서 이어집니다. 이번 포스트에서는 Polya 정리를 1,2,3 차원에서 증명하겠습니다.
Random Walks on Groups - 서론
목차 " data-ke-type="html">HTML 삽입미리보기할 수 없는 소스 제가 최근에 공부한 군 위에서의 랜덤워크 (random walks on groups)의 개요에 대해서 몇몇 포스트를 써보고자 합니다.1. What is it?가장 기본적
sanghn.tistory.com
먼저 지난 포스트에서 언급 했던 랜덤워크의 reccurence를 수학적으로 정의합시다.
(Def) A random walk on a graph is recurrent if $P(W_{n \cdot o}=0 \text{ infinitely often}) = 1$. Otherwise, the random walk is called transient.
즉, 랜덤 워크가 원점 $o$에서 출발한다고 했을 떄, 원점을 무한히 재방문할 확률이 1이라는 것입니다. 즉, 시간이 충분히 흐른다면, 랜덤 워크가 원점으로 돌아오는 것이 보장되는 것입니다.
1. Polya Theorem
이제 Polya 정리를 알아봅시다. Polya 정리는 아래와 같습니다.
(Polya Theorem)
The simple random walk on $\mathbb{Z}^{d}$ is recurrent if and only if $d=1,2$
즉, 시간이 충분히 흐르면, 1차원과 2차원에서는 simple random walk가 반드시 시작점으로 돌아오지만, 3차원 이상부터는 시작점으로 돌아오지 않을 수도 있습니다. 흔히 랜덤 워크를 술에 취한 사람의 움직임에 비유하고는 하는데, 이 정리에 따르면 술에 취한 사람은 반드시 제자리로 돌아오지만, 술에 취한 새는 그렇지 않을 수도 있음을 보여줍니다.

이 정리를 증명하기 위해서는 먼저, 아래의 lemma를 증명해야 합니다.
(lemma)
Let $P^{n}(x,y):=P(W_{n} | W_{o}=x)$ and $m:=\sum_{n \geq 0}P^{n}(0,0)$.
Then, the random walk is recurrent if and only if $m=\infty$
proof) $ P(W_{n} | W_{o}=x) $는 시간이 $n$만큼 지났을 때 랜덤 워크가 원점에 위치할 확률입니다. 따라서, 이 확률을 모든 시간에 대하여 합한 $m$은 0을 방문하는 평균 횟수 (average number of visits to 0)라고 볼 수 있습니다.
이제 $u:=P(\text{walk returns to }0)$라고 하면, $P(\# \text{ visits} \geq k) = u^{k}$가 됩니다. 이는 한번 원점으로 돌아오면, 그전의 경로는 무시하고 새로운 랜덤 워크가 시작되는 것과 같기 때문입니다.
그러면 아래와 같은 결과를 얻을 수 있습니다.
$m=E[\# \text{ visits}] = \sum_{k=0}^{\infty}P(\# \text{ of visits} \geq k) = \sum_{k=0}^{\infty} u^{k} = \frac{1}{1-u}$.
따라서, $m=\infty$는 $u=1$ 과 동치이고, 이는 $P(\text{랜덤 워크가 1번 이상} \; o\text{로 돌아옴})=1$ 과 동치입니다. 또한 이 명제는 $P(\text{랜덤 워크가} \; o\text{를 무한히 많이 재방문 함})=1$ 과 동치가 됩니다.
1 - 1. $d=1$인 경우
위의 lemma에 따라 우리가 보이고 싶은건 $\sum_{k=0}^{\infty}P^{n}(0,0)=\infty$ 이라는 것입니다. 각 step마다 동전을 던져서 왼쪽으로 갈지 오른쪽으로 갈지 결정한다고 하면, 당연히 원점으로 되돌아오기 위해서는 동전의 앞면과 뒷면이 같은 수만큼 나와야 합니다. 즉, 홀수번째 step에서는 $ P^{n}(0,0)=0$ 이기 때문에 우리는 짝수번째 step의 확률만 고려하면 됩니다. 그리고 짝수번째 step에서 앞면과 뒷면의 개수가 같아야 하므로, $n$번째(짝수) step에서 확률은 $ \binom{n}{n/2}2^{-n} $ 가 됩니다.
$P^{n}(0,0)=\begin{cases}
0, \;\; n=\text{odd} \\
\binom{n}{n/2}2^{-n}, \;\; n=\text{even} \end{cases}$
식에서 팩토리얼이 거슬리므로, Stieling's approximation을 이용해 팩토리얼을 지워줍시다.
Stirling's approximation에 따르면, $n! \sim \left( \frac{n}{e} \right)^{n} \sqrt{2\pi n}$ 입니다. 이를 이용하면, 다음과 같은 결과를 얻을 수 있습니다.
$ \binom{n}{n/2}2^{-n} =\frac{n!}{((n/2)!)^{2}} 2^{-n} \approx \frac{\left(\frac{n}{e} \right)^{n} \sqrt{n}}{( \left(\frac{n}{2e} \right)^{n/2} \sqrt{n} )^{2}}2^{-n} = \frac{M}{\sqrt{n}}$
(여기서 $M$은 어떤 상수입니다. Stiring's approximation을 계산할 때 나오는 $\sqrt{2\pi}$들에 대한 계산을 담은 상수입니다. 어차피 스칼라곱은 무한급수의 수렴과 발산에 영향을 주지 않기 때문에 계산의 편의를 위해 무시한 것입니다.)
$\sum_{s=1}^{s=\infty}\frac{1}{n^s}$는 $s \leq 1$ 이면 발산하므로, 위의 결과에 따르면, $\sum_{n \geq 0}P^{n}(0,0) \rightarrow \infty$가 됩니다. 즉, $m=\infty$ 이므로, 위의 lemma에 따라 $d=1$에서 simple random walk가 recurrent 하다는 것을 알 수 있습니다.
1 - 2. $d=2$인 경우
2차원에서의 증명은 다음의 트릭을 사용하면 쉽게 할 수 있습니다. 바로 동서남북의 방향을 정할 때 2개의 독립적인 동전을 던져서 정하는 것입니다. 구체적으로, 첫번째 동전을 던져서 남서(SW)쪽으로 갈지 혹은 북동(NE)쪽으로 갈지를 정합니다. 그리고 두번쨰 동전을 던져서 남동(SE)쪽으로 갈지 북서(NW)쪽으로 갈지를 정하는 것입니다. 그리고 두 동전의 결과를 합치면 동서남북 네 방향중 하나로 이동하게 되는 것이죠. 예를 들어, 북동(NE)와 북서(NW)가 나오면 북쪽으로 이동하는 것입니다.
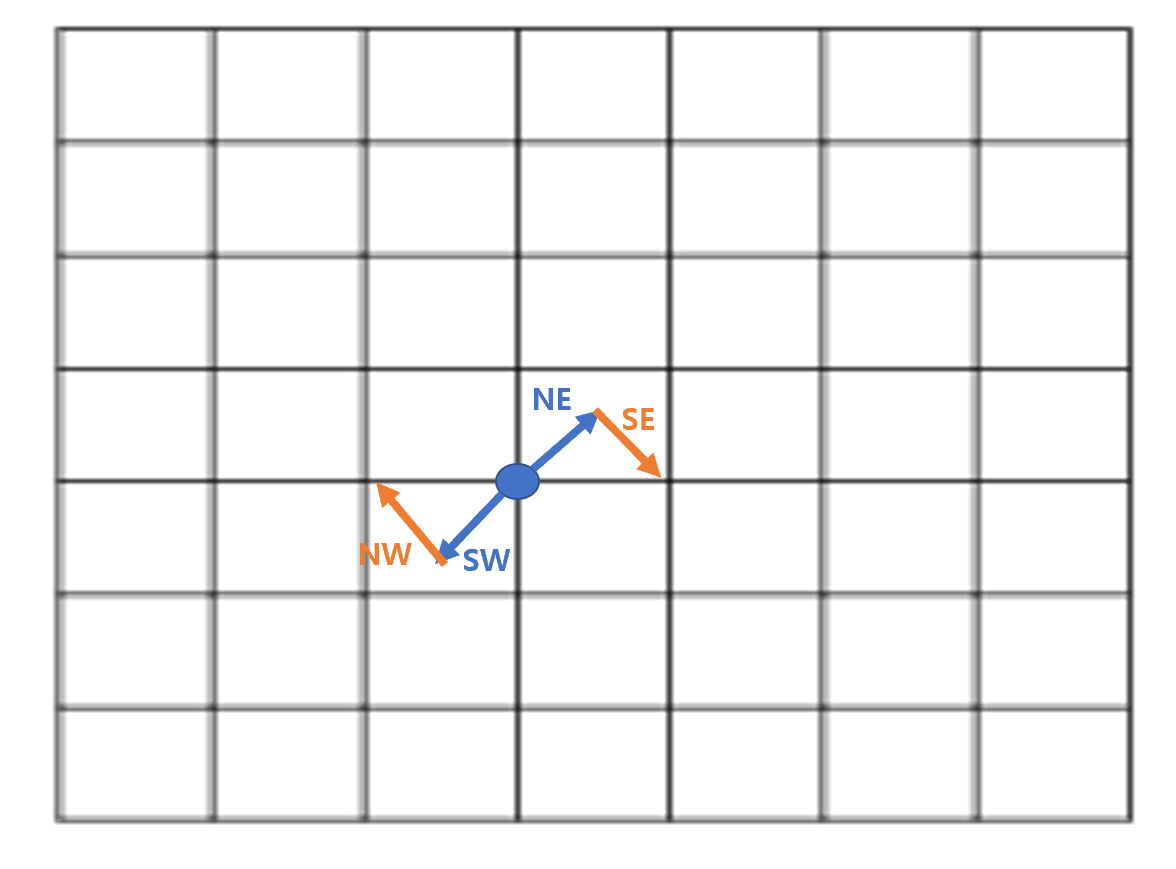
2차원의 경우에도 마찬가지로, 홀수 step에서는 원점으로 돌아오는 것이 불가능 하기 때문에 짝수 step만 고려하면 됩니다. 그러면 아래와 같은 결과를 얻을 수 있습니다. 두 동전이 독립적이었기 때문에 제곱 형태로 바뀌게 되는 것입니다.
$ P^{2n}(0,0) =P( \# NW = \# SE \; \& \; \# NE= \# SW)= P( \# NE= \# SW)^{2} \approx ( \frac{M}{\sqrt{n}} )^{2} = \frac{M^{2}}{n}$
따라서, 조화급수는 발산하므로, $\sum_{n}P^{n}(0,0) \rightarrow \infty$가 됩니다.
즉, 2차원에서도 simple random walk는 반드시 원점으로 돌아옵니다.
1 - 3. $d=3$인 경우
3차원의 경우는 아래 그림과 같은 3차원 grid에서의 움직임을 고려해야 합니다. 아쉽게도 3차원에서는 2차원에서 사용한 트릭을 적용할 수 없습니다. (정육면체의 dual이 정팔면체이기 때문입니다.) 그래서 직접 확률을 계산하도록 하겠습니다.

3차원에서는 아래처럼 기존의 4개의 방향(동서남북)에 2개의 방향(안쪽(I), 바깥쪽(O))이 추가되어 총 6개의 방향으로 움직일 수 있습니다.
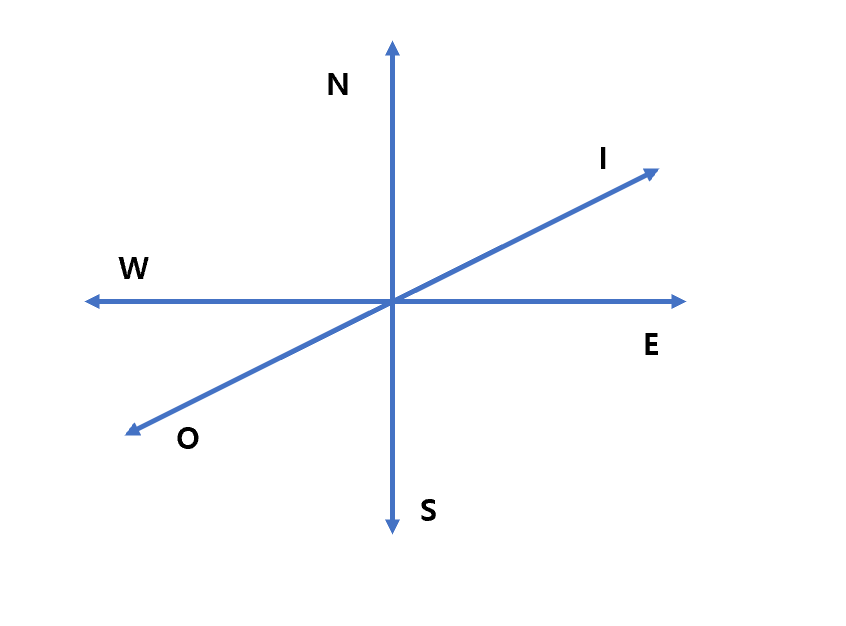
짝수 step만 고려하면 되기 때문에 $P^{2n}(0,0)$만 고려하도록 하겠습니다. $2n$-step에 원점에 위치해 있기 위해서는 남쪽 개수($\#S$)=북쪽 개수($\#N$), 안쪽 개수($\#I$)=바깥 개수($\#O$), 동쪽 개수($\#E$)=서쪽 개수($\#W$)를 만족해야합니다. 그리고 $\#S+\#I+\#E = n$가 됩니다. 그러면 $ P^{2n}(0,0)$은 다음과 같이 생각할 수 있습니다. 먼저, $2n$개의 상자에서 $n$개를 선택합니다. 이제 선택한 $n$개의 상자에는 $S,I,E$를 배치시킬 것입니다. 그러면 먼저, $n$개중에 $k$개를 선택하여 $S$를 배정하고, 그 다음 남은 $n-k$개의 상자에서 $j$개를 선택하여 $I$를 배치하면 됩니다. 그러면 남은 상자에는 자연히 $E$가 배치되게 됩니다. 따라서 $0 \leq k,j \leq n$과 $k+j \leq n$을 만족하는 경우를 모두 더 하면 $2n$-step에 랜덤 워크가 원점에 위치하는 경우의 수가 됩니다.
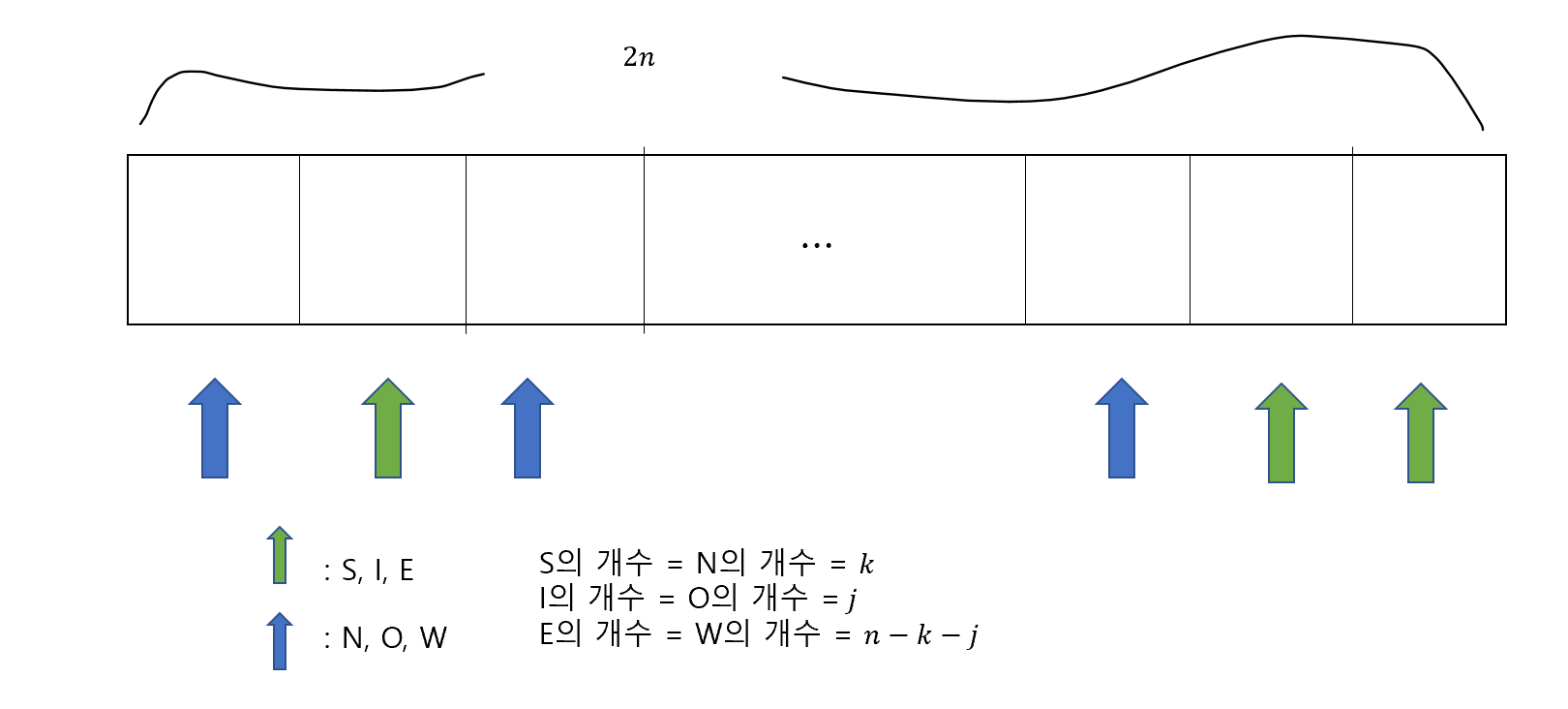
이를 식으로 나타내면 아래와 같습니다.
$P^{2n}(0,0) = 6^{-2n}\sum\limits_{\substack{0 \leq k,j \leq n \\ k+j=n}}\binom{2n}{n}\binom{n}{k}\binom{n-k}{j}= 6^{-2n}\sum\limits_{\substack{0 \leq k,j \leq n \\ k+j=n}}\binom{2n}{n} \left( \frac{n!}{k!j!(n-k-j)!} \right)^{2}$
위의 계산을 직접하면 복잡하므로, upper bound를 이용해서 극한을 계산해보도록 하겠습니다. $\frac{n!}{k!j!(n-k-j)!}$는 삼항계수(trinomial coefficient) 입니다. 이항계수와 마찬가지로 삼항계수 $(a+b+c)^{n}$도 $a,b,c$가 비슷하게 선택되는 경우가 가장 큽니다. 따라서, $\frac{n!}{k!j!(n-k-j)!} \leq \frac{n!}{((n/3)!)^{3}}$가 됩니다. 그러면 아래와 같은 부등식이 성립합니다.
$P^{2n}(0,0) \leq 6^{-2n} \binom{2n}{n} \left( \frac{n!}{((n/3)!)^{3}} \right) \sum\limits_{\substack{0 \leq k,j \leq n \\ k+j=n} } \left( \frac{n!}{k!j!(n-k-j)!} \right) = 6^{-2n} \binom{2n}{n} \left( \frac{n!}{((n/3)!)^{3}} \right) 3^{n} \approx \frac{C}{n^{3/2}}$
($C$: 어떤 상수)
위에서 $\sum\limits_{\substack{0 \leq k,j \leq n \\ k+j=n} } \left( \frac{n!}{k!j!(n-k-j)!} \right)$는 삼항계수의 합이므로, $(1+1+1)^{n}=3^{n}$이 됩니다. 그리고 Stirling's approximation을 사용하여 마지막에 $ \frac{C}{n^{3/2}} $을 얻었습니다. 그러면 $m = \sum_{n=0}^{\infty} P^{2n}(0,0) \leq \sum_{n=0}^{\infty} \frac{C}{n^{3/2}} $이 되고, $\sum_{n=0}^{\infty} \frac{1}{n^{3/2}} $은 수렴하므로, $\mathbb{Z}^{3}$에서 simple random walk는 transient 합니다.
 Skypainter
Skypainter